Algorithmus programmieren?
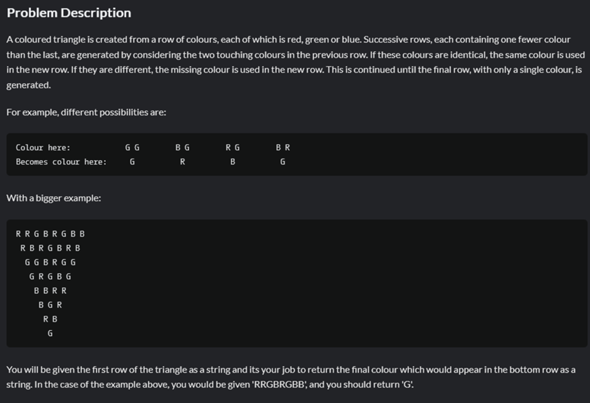
Wie könnte man das effizient lösen?
Der O(n²) Algorithmus ist ja offensichtlich, aber wie geht's in O(n * log(n))?
Das Konzept alleine würde mir schon reichen. Oder ein Stichwort, zu welchem ich recherchieren kann. Ich überlege seit Stunden, aber komme einfach nicht drauf.

Wird denn irgendwo behauptet, dass es in O(n * log(n)) möglich ist?

Ja, indirekt
Der Algorithmus muss 100 verschiedene 100.000 Zeichen lange Wörter in weniger als 10 Sekunden schaffen.
Mit O(n²) ist das unmöglich, selbst mit Zahlen anstatt Buchstaben
4 Antworten

sehe die Farben als zahl :
Rot = 0, blau = 1, grün = 2
Definiere die combine regeln in der Aufgabe folgendermaßen:
combine(x, y) = -x -y mod 3
das das richtig ist sollte man beweisen. (geht einfach in dem man alle möglichkeiten durchgeht)
combine(rot, rot) = -0 -0 mod 3= 0 = rot
combine(blau, blau) = -1 -1 mod 3 = -2 mod 3 = 1 = blau
combine(grün, grün) = -2 - 2 mod 3 = -4 mod 3 = 2 = grün
combine(rot, blau) = -0 - 1 mod 3 = -1 mod 3 = 2 = grün
combine(rot, grün) = -0 - 2 mod 3 = -2 mod 3 = 1 = blau
combine(blau, grün) = -1 - 2 mod 3 = -3 mod 3 = 0 = rot
--
das ist also eine möglichkeit rechnerisch die Farbe zu bestimmen indem man im Körper F3 rechnet.
Jetzt bin ich mir unsicher wie es weiter geht aber es wird wohl in die richtung gehen:
du halso als Input x1, x2, ... xn (das sind die einzelnen letter)
dann hast du wenn du die regel von oben anwendest in der 2. Reihe:
(-x1 - x2, -x2 -x3 , -x3-x4, ...., -xn-1 -xn)
in der 3. Reihe:
(-x1- x2 +x2 +x3 , -x2-x3 +x3 +x4 ,...)usw
und ich denke dadurch kannst du dir eine Formel für das letzte Feld herleiten . Dazu müsste aber ein Stift rausholen und tiefer überlegen.
Hoffe das hilft

Die dritte Reihe wäre x1 + x2 + x2 + x3, x2 +x3 +x3 + x4. Es werden ja beide Seiten negiert.
Aber jo, soweit bin ich auch schon gekommen. Aber dann bin ich wohl auf dem richtigen Weg, danke!
Jetzt nur noch ne Formel dafür finden... Das wird ein Spaß

Das Konzept alleine würde mir schon reichen.
Ich würde das Dreieck auf den Kopf stellen und rückwärts von einem Ergebnis a₁,₁ auf eine gewichtete Quersumme aus a₂ schließen. Im Folgenden bedeutet „=“ immer Kongruenz modulo 3:
a₁,₁ = −a₂,₁−a₂,₂ = a₃,₁−a₃,₂+a₃,₃ = −a₄,₁−a₄,₄ = ...
Diese gewichtete Quersumme ist invariant bei der Reduktion einer Zeile. Berechne sie für eine Eingabe, dann hast Du das Ergebnis a₁,₁.
Die Vorzeichen einer solchen Quersumme entsprechen den Binomialkoeffizienten (mod 3, und bei geraden Zeilen invertiert). Hier siehst Du links das Pascalsche Dreieck (mod 3) und rechts die Vorzeichen der entsprechenden Quersumme:
1 + = +a₁,₁
1 1 − − = −a₂,₁−a₂,₂
1 2 1 + − + = a₃,₁−a₃,₂+a₃,₃
1 0 0 1 − · · − = −a₄,₁−a₄,₄
1 1 0 1 1 + + · + +
1 2 1 1 2 1 − + − − + −
1 0 0 2 0 0 1 + · · − · · +
1 1 0 2 2 0 1 1 − − · + + · − −
1 2 1 2 1 2 1 2 1 + − + − + − + − +
1 0 0 0 0 0 0 0 0 1 − · · · · · · · · − = −a₁₀,₁−a₁₀,₁₀
Ich habe diese „Entsprechung“ für die ersten sieben Zeilen verifiziert. Den allgemeinen Beweis überlasse ich Dir :-)
Wenn dieser Ansatz korrekt ist, brauchst Du für eine Zeile der Länge n nur die passenden Vorzeichen berechnen und damit die gewichtete Quersumme bestimmen. Das sind n Schritte mit je einer Division, bei der ich momentan nicht sehe, wie man die in konstanter Zeit berechnen kann – Schade eigentlich, denn 𝓞(n) wäre auch ganz nett!
Beispiel (mit R=0, G=1, B=2):
Eingabe: 0 0 1 2 0 1 2 2 (n=8)
Pascal: 1 7 21 35 35 21 7 1
mod 3: 1 1 0 2 2 0 1 1
Vorzeichen: − − · + + · − − (1 ist −, da n=8 gerade)
Quersumme: −0 −0 +2 +0 −2 −2 = 1 = G

O(n log) hört sich sehr stark nach Baumstruktur an. Vermutung: Wir gehen zwar jede Zeile durch, aber wir behandeln vorläufig nicht jedes Element, sondern nur die aufteilbaren Paare.
Überlegung: Bei O(n²) benutzen wir - wie bei O(n²) häufig - Informationen doppelt. Wenn wir im Beispiel RR-> und RG->B überführen, benutzen wir das zweite R doppelt. Unnötig.
Wir erstellen also einen Baum!
Und das läuft logischerweise indem wir jeweils die Zeilen teilen. Zuerst wird die erste Zeile geteilt in
RRGB und RGBB
jetzt kümmern wir uns um die erste Hälfte, teilen wieder auf und haben
RR und GB - diese werden nicht mehr aufgeteilt, sondern in R und R umgewandelt.
Beim Zusammenfügen ergänzen wir noch den Rand zwischen R und G, das B und erhalten so RBR. Dito für die andere Hälfte.
Jetzt die Zeitkomplexität: Die Baumstruktur ist klar O(n log(n)), siehe Mergesort. Nur die Frage: Versaut mir meine zusätzliche Prüfung beim Zusammenfügen das O(n log(n))? Da bin ich mir nicht ganz sicher, ich glaube nicht. Aber das nur so als Idee.

RRGBRGBB
->
RRGB RGBB
->
RR GB RG BB
R R B B
Jetzt füge ich das Zeug in der Mitte ein:
R >G R B >R B
Jetzt nochmal das von zwischen RRGB und RGBB
R G R >G B R G
Aber jetzt bin ich wieder am Anfang... Jetzt hab ich wieder 7 Zeichen...
Dann mach ich das ganze nochmal, dann hab ich 6 Zeichen. Usw.
Das kommt also genau aufs selbe hinaus wie der Standard O(n²) Algorithmus.
Oder habe ich was falsch verstanden?

Das war wohl Quatsch, was ich schrieb, denn ich lande mit meinem Quatsch-Algo bei O(n*n*log(n))
Die 2 in theoretischer war wohl doch eher Glück
Verrate uns die Lösung, wenn Sie hast

Haha :D
Ich hatte 'ne 3 glaub ich. Dafür aber in Algorithmen eine 2.
Wobei mich das hier trotzdem überfordert, fühl mich schon richtig dumm xD
Ich glaub der Ansatz von ikmmki geht in die richtige Richtung. Das lässt sich sicher irgendwie als mathematische Formel vereinfachen.
a1, a2, a3, a4, a5
->
a1-a2, -a2-a3, -a3-a4, -a4-a5
->
a1+a2+a2+a3, a2+a3+a3+a4, a3+a4+a4+a5
->
-a1-a2-a2-a3-a2-a3-a3-a4, -a2-a3-a3-a4-a3-a4-a4-a5
->
a1+a2+a2+a3+a2+a3+a3+a4+a2+a3+a3+a4+a3+a4+a4+a5
Jetzt ist die Frage, wie man von a1, a2, a3, a4, a5 direkt auf a1+a2+a2+a3+a2+a3+a3+a4+a2+a3+a3+a4+a3+a4+a4+a5 kommt.
Dann nurnoch ein Modulo 3 dahinter klatschen und fertig.

Und wie kommt das O(log) rein? Von Modulo zu log - das ist mich zu hoch, i am out
Aber liest sich interessant, ich habe die Frage auf Verfolgen gesetzt.
Der Weg scheint gut, im Prinzip müsste es so eine Abbildung geben aus Reihenfolge und Elementen.
viel Erfolg!

Gute Frage. Vielleicht geht's ja auch in O(n), das O(n * log(n)) war nur Intuition, weil es muss halt irgendwas kleines als O(n²) sein. Hab da einfach das nächst-beste gesagt. :P
Aber jetzt bin ich schon einen Schritt weiter
a1+a2+a2+a3+a2+a3+a3+a4+a2+a3+a3+a4+a3+a4+a4+a5
hat folgende Verteilungen:
a1: 1
a2: 4
a3: 6
a4: 4
a5: 1
Hab die einfach mal gegoogelt, Google sagte das ist "Pascal's Triangle".
Wenn ich die Verteilungen weiß kann ich einfach
1*a1 + 4*a2 + 6*a3 + 4*a4 + 1*a5
machen, dann modulo 3, und fertig.
(Jedes a ist ein Wert von 0 bis 2, stellvertretend für "R", "G" und "B". Und am Schluss krieg ich dann auch einen Wert von 0 bis 2 raus.)
Ich glaub ich schau mir dazu mal ein paar Videos an, das dürfte die Lösung sein. Muss halt irgendwie für jedes a(i) ausrechnen, mit was ich es multiplizieren muss. Aber da find ich unterm Stichwort Pascal's Triangle save ein paar Formeln.

Dumm, dass ich das erst jetzt sehe (ich war wohl zu lange mit meiner eigenen Antwort beschäftigt). Dein Ansatz haut tatsächlich hin, und Dein Rechenweg ist praktisch schon der Beweis für das, was ich in meiner Antwort vermutet habe. Genau so wird nämlich das Pascalsche Dreieck berechnet.
Die Binomialkoeffizienten (Zeile im Dreieck) kannst Du leicht iterativ bestimmen:
- (n über 0) = 1
- (n über k) = (n−k+1)/k·(n über k−1).
Beispiel (n=7 für 8 Werte):
- (7 über 0) = 1
- " · 7/1 = 7
- " · 6/2· = 21
- " · 5/3 = 35
- " · 4/4 = 35
- " · 3/5 = 21
- " · 2/6 = 7
- " · 1/7 = 1.
dann modulo 3, und fertig.
Achtung: Die Vorzeichen alternieren mit jeder Zeile. Bei einer geraden Anzahl von Werten musst Du das Ergebnis noch invertieren.
das O(n * log(n)) war nur Intuition
Die Multiplikation (mod 3) könnte man in 𝓞(1) erledigen, aber die Division hängt im Allgemeinen von der Anzahl der Ziffern ab. Den Faktor 𝓞(log n) bekommst Du nur weg, wenn Du für die Berechnung von „(n über k) mod 3“ einen Trick findest.

Divide and Conquer also?
Die Idee hatte ich auch schon. Geht hier leider nicht glaub ich, weil man auch das beachten muss, was dazwischen ist :(
Wenn du RRGBRGBB zu RRGB RGBB aufteilst, dann wird das G, das in der Mitte in den beiden Teilen nicht beachtet, obwohl es den rechtesten bzw. linkesten Buchstaben beeinflusst.
RRGB RGBB
RR BB
^ Hier fehlt in der Mitte was

Siehe bei den Grenzen: Dass dazwischen habe ich meinem Zusatzkommentar ergänzt - ich fülle die Grenzen jeweils beim Baumhoch gehen
Pro Zeile: O(n)
Baum hoch gehen: O(log(n))
--> O(n log(n))
Ich denke, ich liege richtig. Siehe auch meine Herleitung im Kommentar dazu, ich erhöhe stark die Speicherkomplexität, brauche also keine Information zweimal abfragen, sondern bediene mich der gespeicherten Information.
Aber vielleicht liege ich auch falsch.
Dass man es mathematisch verkürzen kann - weiß ich nicht. Das wäre aber Zahlentheorie und nicht theoretische Informatik.

Doch, beim Baum wieder hochgehen füge ich das G mit ein.
Beim Mergesort werden die Teile zum Schluss ja auch zusammengefügt, ebenso bei Quicksort. Und hier wird zusätzlich noch etwas eingefügt, das ist aber sowieso nur O(n). Das Baum-Hochgehen ist O(log(n)).
Korrigiere mich, wenn ich falsch liege.
Oder teste es :-)

original_string = "RRGBRGBB"
def cast_string_to_number(text) -> list:
number_list = []
for letter in original_string:
if letter == "G":
number_list.append(1)
elif letter == "R":
number_list.append(3)
elif letter == "B":
number_list.append(7)
return number_list
def recast(number_list: list) -> list:
color_list = []
for i in number_list:
if i == 1:
color_list.append("G")
elif i == 3:
color_list.append("R")
elif i == 7:
color_list.append("B")
return color_list
def pair(c1: int, c2: int) -> int:
c = c1 + c2
if c == 2:
return 1
elif c == 6:
return 3
elif c == 14:
return 7
elif c == 4:
return 7
elif c == 8:
return 3
elif c == 10:
return 1
else:
# error
return 0
def next_row(row: list) -> list:
new_row = []
for i in range(len(row) - 1):
r = pair(row[i], row[i + 1])
new_row.append(r)
return new_row
if __name__ == '__main__':
pre = cast_string_to_number(original_string)
print(pre)
while len(pre) > 1:
pre = next_row(pre)
print(recast(pre))
liefert das erwartete Ergebnis (geht aber vermutlich um welten effizienter )
Funktion 1: def pair(color1: int, color2: int) -> int
jede farbe hat eine nummer 1, 3, 7 die man addieren kann und die dann zu einer einzigarigen nummer nur aus der kombi führen -> wird am ende wieder übersetz 2 = grün ,6 = rot, 14 = blau , 4 = blau, 8 = rot, 10 = grün
wird per match gehandelt
Funktion 2: def next_string(text: str,) -> str
hier wird der string zu einem string mit einem buchstaben weniger gemacht
new_text = ""
for i in range(len(text) - 1):
a = text[i]
b = text[i + 1]
// hier ein match um die buchstaben zu den zahlen grün = 1, rot = 3, blau = 7
number = pair(a, b)
// match handler um number wieder zu einem buchstaben zu machen (new_letter)
// zum string hinzufügen
text += new_letter
// nach der for loop
return new_letter
so kannst du jetzt mit der funktion 2 den string zum kombinierten nächsten machen
in der main Funktion gehst du hin und lässt den string in einer schleife while len(text) > 1
in der Funktion 2 durchlaufen
und überschreibst so immer wieder text. am ende hast du dann deinen string

Das ist leider O(n²), weil zwei Schleifen ineinander.
Glaub das Problem ist eher mathematischer Natur, mit Modulo 3 und so n Zeug.

Angenommen der String hat 100.000 Zeichen, dann läuft das ja
100.000 Durchgänge (äußere Schleife. len(text) wird jeden Durchgang ja nur um 1 weniger)
*
50.000 Buchstaben (im Durchschnitt. Anfangs 100.000, am Ende 1, nimmt linear ab, also 50k im Schnitt)
=
5.000.000.000 pair-Aufrufe.
Das braucht wahrscheinlich Stunden bis es fertig ist. :D

nein so langsam ist das nicht. also so einfache operatioenn durchzuführen geht vermutlich relativ schnell

hab die antwort aktualisiert dass ganze geht aber ist zwar nicht best practice. 50k lange strings sollten gehen
ich schaue mal wielange das so dauert

trotzdem ist dein Algorithmus proportional zur quadratischen Eingabe länge und der Fragesteller mein es geht auch in O(log(n) * n)

ja okay kann sein, hab ja gesagt ist nicht best practice aber es geht halt. Also meiner meinung nach besse wie gar nichts xD

Das darf für ein 100.000 Zeichen langes Wort aber nur 0.1 Sekunden brauchen.
Angenommen diese pair Funktion ist super effizient und dein PC schafft davon 100.000.000 Durchläufe pro Sekunde, dann braucht das trotzdem noch 50 Sekunden.
Mit O(n²) schlichtweg unmöglich, da kann der Code noch optimiert sein.
Aber trotzdem danke.

okay welche sprache machst du das ganze denn? weil zB bei python solltest du dann eine lib fürs iterieren nutzen weil die meist in c sind und so viel schneller da kannst du auch noch zeit sparen aber ansonsten ist mein algorithmus vermutlich eh nicht effizient. ist ja wie wenn man sich einen eigenen primzahlen algorithmus überlegt

JavaScript. Also fast so langsam wie Python :D
Also Baumstruktur klar O(n log). Das Zusammenfügen passt ganz am Ende von unten nach oben und kostet mich im Beispiel
Teilen (O(log (n)):
RRGBBGBB
RRGB BGBB
RR GB BG BB
Herrsche 1 - die Umwandlung der Teile (O(n)):
R R R B
Herrsche 2 - die Grenzen: Hier jetzt der Grenzcheck
R + (R+G-->B) + R + (B + B-->B) + R + (G + B--> R) + B
Das kostet mich pro Zeile O(n). Das ganze mache ich jetzt den Baum hoch, ist also O(n * log(n))
Aber wie spare ich mir das Stück von O(n log(n))? Durch Speicherkomplexität, ich muss nämlich permanent den Baum gespeichert halten ...
Und in der Klausur theoretische Informatik hatte ich nur ne 2, ärgerlich! Aber vielleicht ist das hier ja auch der allerletzte Müll und die 2 absolut überzeichnend ...