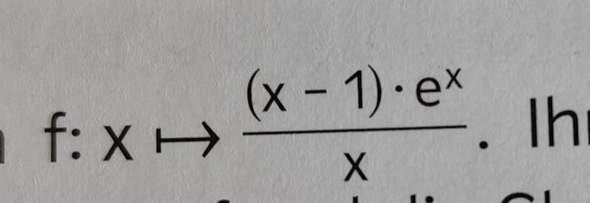Hat der Professor recht?
Hallo, es geht um Fehlerrechnung. In den Folien des Profs steht: Für x gebe es 3 gleiche Werte. Also: x1= 4 , x2=4, x3=4 Jede der Werte habe eine konstante Messunsicherheit von DeltaX=0,1 So berechnet sich der Fehler des Mittelwerts aus X: Mittelwert X = 4 Fehler des Mittelwerts = Wurzel( [0,1]²+[0,1]²+[0,1]² ) Ende. Müsste man aber für den Fehler des Mittelwerts bei bekannten einzelnen Fehlern nicht das Ergebnis aus der Wurzel durch Anzahl der Messwerte teilen? In diesem Fall also 1/3 mal Wurzel( [0,1]²+[0,1]²+[0,1]² ) Sehr wahrscheinlich hat der Prof es richtig, wollte aber fragen