y/(x^2+y^2) wie kann ich diese Funktion auf Stetigkeit überprüfen?
gehe davon aus dass es nicht stetig ist müsste also zeigen das lim n--> unendlich f(an) = f(lim n--> unendlich an) gelten muss wobei an eine beliebige Folge ist beispielsweise (1/n, 1/n) . Aber wenn ich beispielsweise 1/n als Folge nehme kommt unendlich raus also muss es wahrscheinlich einen anderen Weg geben.
3 Antworten
Du nimmst eine Folge (xn,yn) mit xn->0, yn -> 0, aber f(xn,yn) nicht gegen 0.
Und das geht gut mit xn = yn = 1/n, dann hast du
f(xn,yn) = 1/n / (1/n^2 + 1/n^2) = n/2, und diese FOlge divergiert, daher ist die Funktion in (0,0) nicht stetig (in allen anderen Punkten selbstverständlich schon)
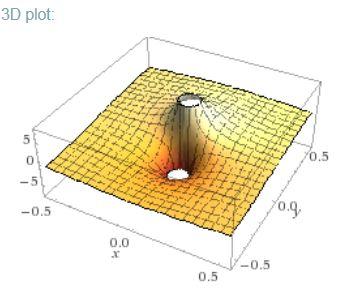
Deine Funktion ist überall stetig. An den beiden Polstellen ist sie nicht definiert:
http://www.wolframalpha.com/input/?i=y%2F%28x%C2%B2%2By%C2%B2%29
Wenn unendlich rauskommt, ist die Funktion insbesondere nicht stetig.
Also hätte dann 1/n/2/n^2 und dann n^2/2n. Dann kürzen n/2 und das würde ja gegen unendlich gegen damit hätte ich Unstetigkeit schon bewiesen ?