Stetigkeit von cos 1/x?
Hallo zusammen,
ich hänge gerade an der Frage der Stetigkeit von cos 1/x. Es wird behauptet, dass für x=0 die Funktion unstetig ist aber sonst ist sie stetig. Das müssen wir dann zeigen. Wollte das dann mit dem Epsilon-Delta-Kriterium machen, weiß aber noch nicht wie.
Danke schonmal im Vorraus
3 Antworten
Es wird behauptet, dass für x=0 die Funktion unstetig ist aber sonst ist sie stetig.
Das stimmt so nicht. Die Funktion ist an der Stelle x = 0 weder stetig noch unstetig, da sie dort überhaupt nicht definiert ist.
================
Die Funktion
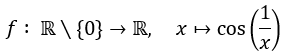
ist stetig. Begründung: Die Funktion ist eine Verkettung der stetigen Funktionen
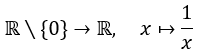
und
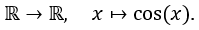
(Verkettungen stetiger Funktionen sind stetig.)
================================
Was nun evtl. gemeint sein könnte: Ist die Funktion
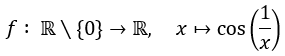
an der Stelle x = 0 stetig fortsetzbar? Also: Gibt es ein y₀ ∈ ℝ, sodass die Funktion
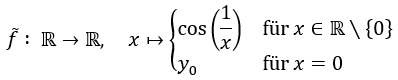
stetig ist? Dies wäre genau dann der Fall, wenn der Grenzwert
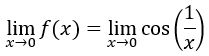
existieren würde. Dann wäre y₀ dieser Grenzwert. Allerdings existiert dieser Grenzwert nicht. Denn...

Demnach ist die Funktion an der Stelle x = 0 nicht stetig fortsetzbar.
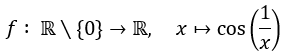
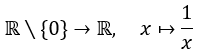
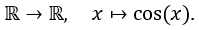
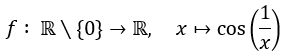
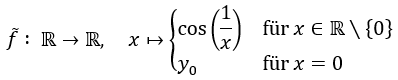
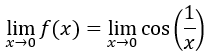

So weit ich den Überblick habe, stellt die Funktion eine Reihe von U's dar, die bei Pi/2, 1 1/2 Pi, 2 1/2 Pi usw. unendlich sind und bei 0, 2 Pi, 4 Pi usw. als Ergebnis 1 haben, bei Pi, 3Pi, 5 Pi usw. als Ergebnis -1 haben. Das U zwischen - 1/2 Pi und + 1/2 Pi ist ein U, die U's daneben umgedreht, dann wieder als U's usw.
Pardon, aber ich habe nur einen Hauptschulabschluss mit Hängen und Würgen. Habe nur geantwortet, weil ich die Frage interessant finde.
Stell doch mal eine Wertetabelle auf!
Tipp: Finde zwei Teilfolgen, die gegen unterschiedliche Grenzwerte konvergieren.
Wie finde ich die Teilfolgen?