Wurzelfunktion zwei Werte?
Eigentlich hat eine Funktion zu jedem x-Wert ja maximal einen y-Wert.
Auch Wurzelfunktionen wurden in der Schule immer so dargestellt, dass z.B. für alle Werte oberhalb der x-Achse sind.
Aber die Wurzel hat ja immer zwei Werte, für 4 z.B. 2 und -2, die Funktion müsste also für alle positiven x-Werte zwei y-Werte haben. Gibt es eine Definition hierfür, die das ausschließt und zudem festlegt, dass immer das positive Ergebnis der Wurzelfunktion genutzt wird?
4 Antworten
Aber die Wurzel hat ja immer zwei Werte, ...
Nein, hat sie nicht, weit verbreiteter Irrtum...
Korrekt wäre:
Die Gleichung x² = n hat immer zwei Lösungen, nämlich die positive und die negative Wurzel von n.
Die Wurzel in n ist immer (per Definition) die positive Lösung dieser Gleichung.
Gibt es eine Definition hierfür, die das ausschließt und zudem festlegt, dass immer das positive Ergebnis der Wurzelfunktion genutzt wird?
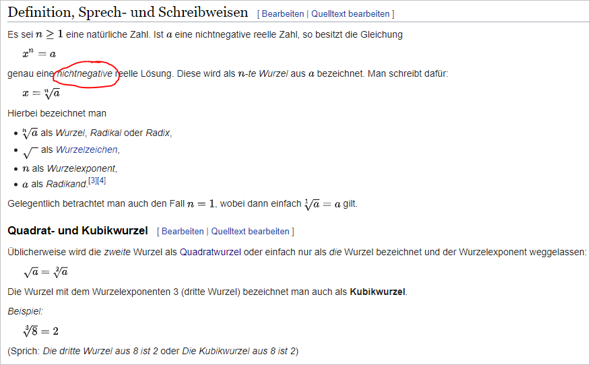
Ja, schau dir doch einfach mal Definitionen der Wurzel an. Da wird in der Regel extra definiert, dass es sich um den nichtnegativen reellen Wert handelt, was den entsprechenden negativen Wert dann ausschließt und die Eindeutigkeit des Funktionswertes gewährleistet.
Wenn man also √(4) schreibt ist damit nur 2 gemeint, und nicht -2.
Definitionen auf Wikipedia als Beispiel:

https://de.wikipedia.org/wiki/Wurzel_(Mathematik)


Ja, die Wurzelfunktion ist so definiert, dass sie nur positive Werte (oder 0) liefert. Man muss also immer schreiben
+-√3
Ja, man definiert die Wurzel aus x als diejenige nicht-negative Zahl w, die w² = x erfüllt, damit die Wurzelfunktion wirklich eine Funktion ist.