Wie könnte die Funktionsgleichung dieses Graphen lauten?

Es geht darum dass ich die 1. und 2. Ableitung angeben muss (auch graphisch!)
2 Antworten
das ist ein logistisches wachstum mit der sâttigungsgrenze ~10 und einem wendepunkt bei ca. 6=x
Guck im internet nach logistisches wachstum formel. Dort die genannten zahlen einfach korrekt einsetzen
viel spass
Es sieht so aus, also könnte die Funktionsgleichung beispielsweise
lauten.

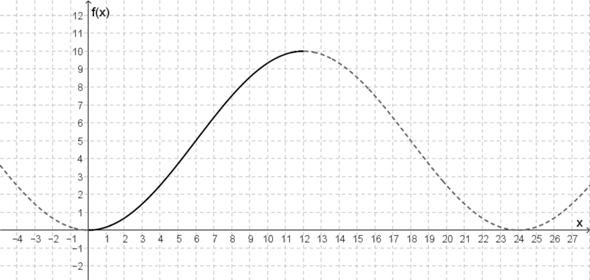
Naja, ich habe mir einfach überlegt, welche Funktionen ich kenne, die Bereiche habe, in denen der Graph zunächst flach verläuft, dann antsteigt und dann wieder abflacht. Da sind mir dann die Sinus- bzw. die Kosinus-Funktion eingefallen. Dann habe ich die Funktionsgleichung einer Kosinus-Funktion so angepasst, dass der entsprechende Bereich des Graphen entsprechend gestreckt und verschoben wurde, sodass der entsprechende Graph-Bereich bei (0, 0) beginnt und bei (12, 10) endet.
Es geht darum dass ich die 1. und 2. Ableitung angeben muss (auch graphisch!)
Wenn es darum geht, die 1. und 2. Ableitung zu skizzieren, braucht man dafür nicht unbedingt die Funktionsgleichung. Viel mehr geht es dann wahrscheinlich darum, dass du erkennen sollst, was die 1. Ableitung bzw. die 2. Ableitung anschaulich bedeuten.
============
Die 1. Ableitung gibt quasi die Steigung an. Da kann man dann erkennen, dass die Funktion zunächst Steigung 0 hat, dann die Steigung zunimmt, bis sie bei etwa x = 6 maximal wird. Danach nimmt die Steigung wieder ab, bis sie bei x = 12 wieder 0 ist.
Dementsprechend beginnt die erste Ableitung bei (0, 0) und steigt dann an, bis sie bei etwa x = 6 ein Maximum hat. Dann nimmt die erste Ableitung ab, bis sie bei (12, 0) wieder gleich 0 ist.
============
Die 2. Ableitung gibt quasi das Krümmungsverhalten an, da sie die Änderungsrate der 1. Ableitung beschreibt.
Wenn die 2. Ableitung positiv ist, ist der Graph der ursprünglichen Funktion linksgekrümmt, da die 1. Ableitung (und damit die Steigung der ursprünglichen Funktion) zunimmt.
Wenn die 2. Ableitung negativ ist, ist der Graph der ursprünglichen Funktion rechtsgekrümmt, da die 1. Ableitung (und damit die Steigung der ursprünglichen Funktion) abnimmt.
Im konkreten Fall... Der Graph ist zunächst linksgekrümmt, also die 2. Ableitung positiv. Die Linkskrümmung wird dann schwächer, bis sie an einem Wendepunkt in eine Rechtskrümmung wechselst. Der Wendepunkt befindet sich bei etwa x = 6. Dementsprechend wechselt die 2. Ableitung bei etwa x = 6 vom Positiven zum Negativen.
============
Hier ein Bild, wie die Graphen der 1. Ableitung bzw. 2. Ableitung aussehen:
https://i.imgur.com/uAWEDbD.png
Naja. Man könnte auch beispielsweise die Gleichung...
f(x) = 5/24 x² - 5/432 x³
...finden, welche den Graphen beschreiben könnte.
Siehe auch: https://i.imgur.com/uDsBOPY.png
Woran erkennst du das?