wie kann man eine solche aufgabe lösen?
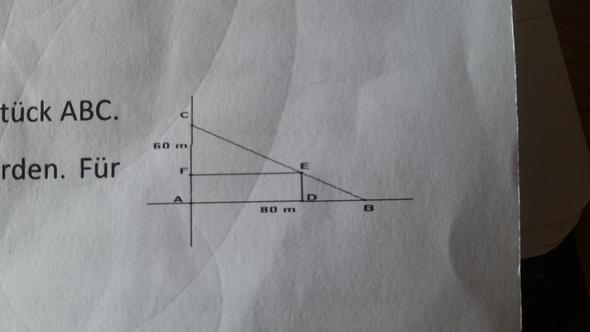
"Zwischen sich zwei rechtwinklig kreuzenden Straßen liegt ein dreieckiges Grundstück ABC. auf diesem soll ein möglichst großer, rechteckiger Bauplatz ADEF abgestreckt werden. Für welche Lage von E wird die Fläche am größten?" so in etwa weiß ich schon wie man solche aufgaben löst, nur bei dieser bin ich auch nach 2h auf keinen punkt gekommen :/
8 Antworten
Hallo,
wie andere hier schon geschrieben haben, handelt es sich hier um eine sogenannte Extremwertaufgabe. Du hast also eine Funktion, von der nicht nur der Graph gesucht wird, sondern bei der bestimmte Werte einen maximalen oder minimalen Wert annehmen sollen. Für den gesuchten Extremwert wird eine sogenannte Nebenbedingung formuliert.
Zunächst einmal brauchst Du die Funktionsgleichung für die Gerade, auf der E liegt. Eine Gerade hat im allgemeinen die Gleichung y=mx+b.
Mit b ist der Punkt gemeint, an dem die Gerade die y-Achse schneidet - in Deinem Fall ist das 60. Also: b=60
Mit dem m ist die Steigung der Geraden gemeint. Wenn es von links nach rechts bergauf geht, ist die Steigung positiv, wenn es bergab geht, negativ.
Wenn die Gerade flach ist, also entweder die x-Achse oder eine Parallele zu ihr, ist die Steigung m=0.
In Deinem Fall ist die Steigung, also m, negativ.
m kannst Du nach der Formel (y₂-y₁)/(x₂-x₁) berechnen.
Hierbei sind x und y die Koordinaten von zwei Punkten, die auf dieser Geraden liegen.
Diese zwei Punkte kannst Du am Funktionsgraphen ablesen.
P₁ ist (0|60) und P₂ ist (80|0). Beim ersten Punkt schneidet die Gerade die y-Achse, beim zweiten die x-Achse.
Nun mußt Du die Koordinaten nur noch in die Formel eingeben:
m=(0-60)/(80-0), denn x₁=0, x₂=80, y₁=60 und y₂=0.
m ist also -60/80. Das kannst Du kürzen und erhältst -3/4
Die Gleichung für Deine Gerade lautet also y=(-3/4)x+60
Nun brauchen wir die Nebenbedingung. Innerhalb des Dreiecks zwischen der Geraden und den Achsen soll ein möglichst großes Rechteck entstehen. Die Fläche eines Rechtecks wird nach der Formel F=x*y berechnet. Diese Fläche soll maximal werden.
Jetzt bringen wir unsere beiden Funktionen zusammen:
Oben heißt es: y=(-3/4)x+60
Diesen Ausdruck für y setzen wir nun in die Rechtecksformel ein, damit wir nur noch eine Unbekannte haben. Du ersetzt also in x*y das y durch (-3/4)x+60 und schreibst: f(x)=x*[(-3/4)x+60].
Nach dem Ausmultiplizieren steht da: f(x)=(-3/4)x²+60x.
Hier hast Du die Funktion, zu der Du den Maximalwert - oder, da es sich hier um eine quadratische Gleichung handelt - den Scheitelpunkt suchst.
Für die x-Stelle des Scheitelpunktes gibt es aber eine einfach zu merkende Formel, nämlich: -b/2a
a ist dabei die Zahl, die vor dem x² steht. Wenn keine Zahl davor steht, ist a=1, wenn nur ein Minus vor dem x² steht, ist a=-1.
Hier ist a=-3/4 und 2a ist gleich -3/2
b ist natürlich 60.
So liegt der Scheitelpunkt und damit der Extremwert dieser Parabel bei
-60/(-3/2)
Minus geteilt Minus ergibt Plus, Du kannst die beiden Minuszeichen also weglassen: 60/(3/2)
Eine Zahl wird durch einen Bruch geteilt, indem sie mit dessen Kehrwert multipliziert wird: 60*(2/3) oder 120/3 oder 40
Der Scheitelpunkt liegt also bei x=40.
Nun brauchst Du noch den dazugehörigen y-Wert. Den erhältst Du, indem Du die 40 anstelle von x in die Geradengleichung einsetzt:
y=(-3/4)*40+60, also:
y=-30+60, bzw.:
y=30
Die Fläche des gesuchten Rechtecks ist als 40m*30m=1200 m² groß.
Das ist die maximale Fläche eines Rechtecks, das in das gegebene Dreieck eingeschrieben werden kann.
Herzliche Grüße,
Willy
Die beiden Seiten AB und AC bieten sich hier als Koordinatenachsen an, AB soll nun die x-Achse sein und AC die Y-Achse. Somit ist die Seite CB als lineare Funktion zu betrachten. Diese hätte die Gestalt:
g(x)= mx +n II n= IACI , für m bräuchtest du jetzt einfach noch einen 2. Punkt
Wenn wir nun das Rechteck betrachten merken wir, dass die Fläche berechnet wird durch:
A= Länge * Breite
Die Länge entspricht hierbei der x-Koordinate des Eckpunktes auf der Geraden und die Breite der Y-Koordinate. Der Eckpunkt P wäre dann gegeben durch: P ( x I g(x) ) ;
und daraus Folgt für die Fläche des Rechteckes:
A(x)= x*g(x) = mx² +n*x
Nun gilt es diese Funktion auf Extrema zu untersuchen:
A(x)= mx² +n*x
A´(x)= 2mx +n
Notwendige Bedingung: A´(x)= 0
0 = 2mx +n II -n II *1/2m
-n/2m = x
Hinreichendes Kriterium; A´´(x) ungleich 0 und A´(x)=0
A´´(x) = 2m II m<0 da der Graph fällt
---> A´´(x)< x --> Maximum
Einsetzen in die Ausgangsgleichung:
A(-n/2m) = (n/4m) - (n²/2m)= (n/2m)*[ (1/2) - n]
Daraus folgt, dass die größte Fläche folgende Maße besitzt:
Länge: -n/2m
Breite: g(-n/2m)
Fläche: A= (n/2m)*[ (1/2) - n]
jetzt kann ich wieder nicht abschicken; und der macht mir die ganze schöne Formatierung kaputt. Was ich hier schon für Scherereien hatte.
Die horizontale Katete sei p ( wie parallel ) und die vertikale s ( wie senkrecht ) Die Linkeckseiten bezeichne ich mit x und y ; das Problem wird zurück geführt auf zwei dimensionslose Zahlen:
x =: ß p ( 1a )
y =: µ s ( 1b )
Dann hast du die Extremalbedingung für die Rechteckfläche
F ( ß ; µ ) := ß µ = max ( 2 )
Die Nebenbedingung liest man aus dem Strahlensatz ab.
s / p = y / ( p - x ) ( 3a )
Jetzt einsetzen von ( 1ab ) in ( 3a )
µ
s / p = ( s / p ) ---------------- ( 3b )
1 - ß
ß + µ = 1 ( 3c )
wir transformieren in den abstrakten ( ß ; µ ) Raum. ( 2;3c ) lautet in Worten: Unter allen Rechtecken mit Seite ß bzw. µ so wie Umfang = 2 bestimme das flächengrößte. Die Lösung kennt ihr; das Quadrat ( in diesem abstrakten Raum. )
ß = µ = 1/2 ( 3d )
Damit hat Röderich von Rödelheim Recht. Und ich kannte mal " Eppo von Eppstein " , einen ===> Dalmatiner. Der boll nur nachts ganznächtig von 22 - 6 h und hatte Frauchen ins Bein gebissen. Versteh ich nich; Kinder kommen doch VOM STORCH und nicht AUF den HUND . Und Herrchen nieste statt " Hatschi " immer " Peia " ; das wurde dann selbst redend sein Spitzname. Aber dann erwirkte der Peia ein höchstrichterliches Urteil. Es erfülle den Tatbestand der Beleidigung, eine BELIEBIGE Person als Peia zu titulieren. Also sieh dich vor ...
Lass den Punkt auf der Geraden wandern. Die Fläche A des Rechtecks ist an jeder Stelle x * y. Für y setzt du die Geradengleichung ein. (ich hoffe, du kennst die Achsenabschnittsform, sonst musst du mit m und b darangehen.)
Für die Fläche A ergibt sich eine quadratische Gleichung. Du kannst A'(x) bilden und bei A'(x) = 0 erhältst du den x-Wert, der hier nur das Maximum sein kann. Nicht vergessen, y auszurechnen, damit du die maximale Fläche errechnen kannst.
Sei E(x | y). Nach dem Strahlensatz ist AC : AB = DE : DB →
60/80 = y/(80 - x) → y = ¾(80 - x) = 60 - ¾x
Fläche Φ = xy = 60x - ¾x² → Φ‘ = 60 - 1,5x und aus Φ‘ = 0 folgt x = 40 → y = . . .