Wie kann ich an einem Graphen erkennen, ob es zu EINER Funktion gehört oder nicht?
Hey Leute, wir haben heute ein neues Thema in Mathe gestartet, jedoch bin ich noch unsicher darin. Ich verstehe nicht, wann ein Graph bloß zu einer Funktion gehört, bzw. wann ich dies erkenne. Ich habe hier auch was hochgeladen. Wäre sehr nett, wenn ihr mir zu den einzelnen Graphen erklären könntet, wie Ihr darauf gekommen seid, damit ich es besser nachvollziehen kann. Danke im Voraus!
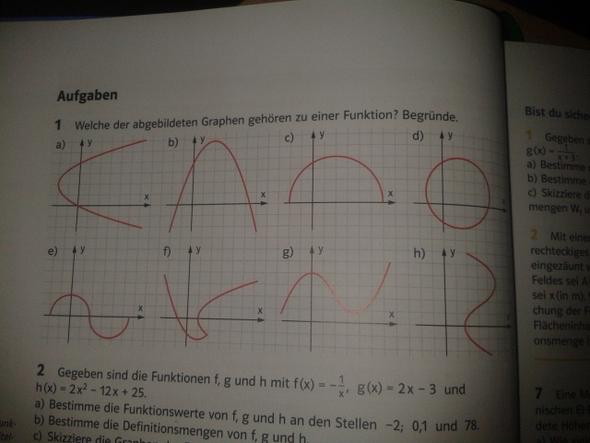
5 Antworten
Wenn du die y-Achse nach rechts und links verschiebst, darf die y-Achse - salopp gesprochen - nicht mehr als einmal den Graphen schneiden oder berühren.
Stell dir vor, du gehst wie mit einem Scanner von links nach rechts mit der y-Achse darüber.
Das gilt für Winkelfunktionen, nicht für bogenfunktionen, denn da ist es umgekehrt, da darf für 1 y-Wert nur 1 x-Wert existieren! a) ist eine Wurzelfunktion und h ist eine Arkussinus-Funktion!
Ich weiß nicht, ob ich dich richtig verstanden habe, aber die Arkussinus-Funktion ist eine Umkehrfunktion. Normalerweise kann es zur Sinusfunktion keine Umkehrfunktion geben, da sie nicht bijektiv ist. Deswegen beschränkt man sich bei den Rückgabewerten der Arkussinusfunktion auf ein bestimmtes Intervall.
Der Graph h) ist im strengen, mathematischen Sinn kein Bestandteil einer Funktion, sofern x die Variable ist, von der f abhängt.
Die Frage ist nicht, ob der Graph zu genau einer Funktion gehört, sondern, ob der Graph zu einer Funktion gehören kann oder nicht. Eine Zuordnung ist dann eine Funktion, wenn jedem x-Wert genau ein y-Wert zugeordnet wird. Die y-Werte sind durch die rote Linie eingetragen, die dazugehörigen x-Werte sind die genau senkrecht darunterliegenden Werte auf der x-Achse.
Du suchst also all jene Graphen, bei denen über jedem x-Wert nur ein einzelner roter Punkt ist. sobald es zwei oder mehr sind, ist es keine Funktion mehr. b zum Beispiel stellt eine Funktion dar, a aber nicht, denn bei a hast du z.b. bei x = 0 zwei y-Werte.
Danke für die Korrektur. Ich glaube ich habe das verstanden, Also sind doch die Graphen a, d, f und h KEINE Funktion? Vielen lieben Dank!
Wenn der Graph zwei mal die y achse trifft ist es keine funktion. Ebenso nicht wenn zwei punkte senkrecht übereinander sind z.B: 3 und -3 oder 2 und -2
a,b,c = Parabel -> x²
e,g,h= x³
d,f sind keine Standardfunktionen
Die Formen muß man einfach kennen.
Haben heute erst das Thema gestartet, wie bereits erwähnt, deswegen kenne ich eine Form wie x³ noch nicht :) Das heißt also das alle Graphen bis auf d und f eine Funktion sind? Oder hab ich das jetzt falsch verstanden ?
wenn senkrecht nach oben z.B. zwei punkte übereinander sind, ist es keine funktion.
Das heißt, Graph a, d, f und h sind KEINE Funktion? Oder hab ich da was falsch verstanden ?
Vielen lieben Dank für deine Hilfe! Soweit ich das nun verstanden habe, sind die Graphen a, d, f und h KEINE Funktion, ist das richtig ? :)