Mathe Graphen Funktionen?
Hallo ihr lieben,
Ich sitze an meinem Mathe Hausaufgaben und komme nicht weiter! Ich soll anhand der Graphen erkennen was eine Funktion ist und was nicht! Soll zu jedem Graphen auch eine kurze Erklärung geben.
Danke im
Voraus
4 Antworten
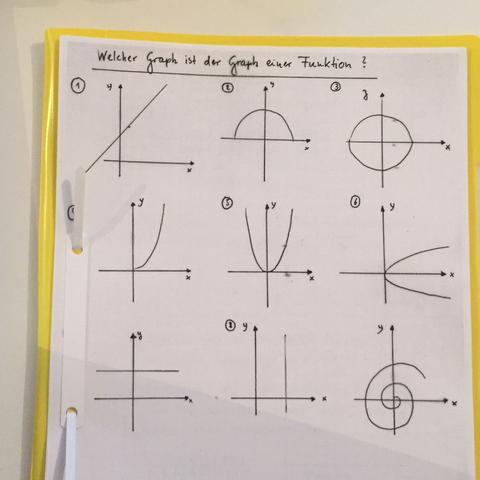
1) Lineare Funktion: Sie hat sowohl kein Anfang als auch kein Ende. Funktion: f(x)=mx+b
2) (unsicher) Parabel, Funktion wäre: f(x)=-mx^2+b (-m weil die Parabel "nach unten zeigt", x^2 weil es eine Parabel ist)
3) ein Kreis kann keine Funktion sein
4) Müsste eine Wurzelfunktion sein, mehr kann ich leider auch nicht dazu sagen
5) scheint eine Normalparabel zu sein: f(x)=x^2
6) (unsicher) müsste f(y)=y^2 sein tendenziell, aber wenn man von f(x) ausgeht dann ist es keine Funktion
7) Lineare Funktion: f(x)= b
8) Keine Funktion
9) ist keine Funktion :D
Nimms mir nicht übel, ich bin nur n Schüler und war grade froh dass ich es erstmal hinter mir habe. Ansonsten hab ich nachgeguckt, bei Mathebibel und bei frustfrei-lernen, kann man das alles sehr gut nachlesen (kann dir leider nicht die Seiten schicken, da die Antwort sonst als Spam gekennzeichnet wird)
Eine Funktion hast du, wenn jedem x-Wert genau ein y-Wert zugeortnet wird. Sobald ein x-Wert also 2 oder mehr y-Werte hat, stellt der Graph keine Funktion mehr da.
3, 6, 8 und 9 sind demnach keine Funktionen.
Das mit der "kurzen Erklärung" habe ich übersehen^^
1) lineare Funktion: y=mx+b
m: Steigung, b: y-Achsenabschnitt
2) Halbkreis: y=√(r²-x²)
r: Radius
4) Parabel mit begrenztem Definitionsbereich ID = {x∈IR | x≥0}:
y=a(x²-d)+e
a: Streckfaktor, Scheitelpunktkoordinaten (d|e)
5) Parabel: y=a(x²-d)+b
a: Streckfaktor, Scheitelpunktkoordinaten (d|e)
7) lineare Funktion mit der Steigung 0: y=b
b: y-Achsenabschnitt
3,6,9 sind keine. Eine Funktion kann keine 2 y Werte an einem x-Wert haben.
Graph 1 ist eine lineare Funktion
Graph 2: ist eine Parabel (quadratische Funktion)
Graph 3: ist der Einheitskreis (aber ist das eine Funktion? ich glaube nicht)
Graph 4: ist eine Parabel, wo für die x-achse nur positve Werte zulässig sind
Graph 5 ist eine Parabel
Graph 9 ist keine funktion