Wie erkenne ich ob der Graph eine Funktion ist oder nicht?
Hey, mache gerade meine Mathe HA. Und ich check echt nicht woran mann erkennt ob der Graph eine Funktion ist oder nicht.. kann mir jemand helfen?
4 Antworten
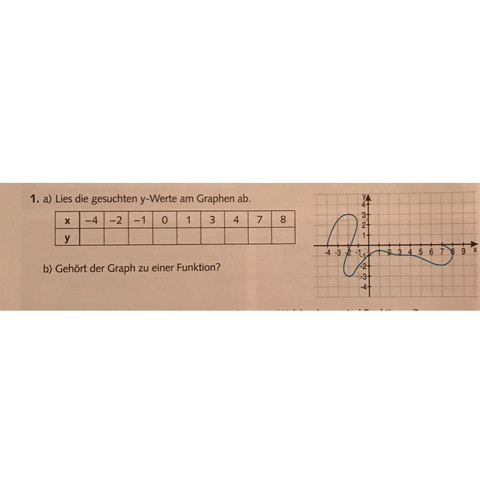
Vereinfacht gesagt, ist der Graph eine Funktion, wenn bei jedem x-Wert
nur genau 1 y-Wert dabei ist. In deinem Beispiel in der Zeichnung ist an
der Stelle x = -2, der Graph sowohl beim y-Wert = +3 als auch beim
y-Wert = -3, es sind also sozusagen 2 Punkte an der gleichen Stelle
"übereinader" und das darf auch nicht sein.
Wenn es keine zur y-Achse parallele Gerade gibt, die den Graph in mehr als einem Punkt trifft, liegt ein Funktionsgraph vor.
Du kannst also ein Lineal nehmen und mit diesem (während es stets zur y-Achse parallel bleiben soll) den gesamten Graph von links bis rechts "durchkämmen" und dabei auf diese Bedingung prüfen. Das Lineal stellt dabei natürlich nur einen Ausschnitt der zur y-Achse parallelen Gerade dar.
gibts zu jedem x genau einen y wert?
falls ja: funktion
falls nein: keine funktion
praktisch wirst du in der schule nie eine nicht-funktion treffen, denn die lässt sich nicht als funktionsvorschrift (daher der name!) schreiben! :-)
bspw.
x^2+y^2=1
ist keine funktion denn zu x=0 existieren y=1 und y=-1, also 2 bilder.
daher keine funktion.
das ganz ist übrigens nicht zu verwechseln mit den ...jektivitäten.
bei der funktionsfrage gehts drum:
gibts zu jedem urbild genau ein bild?
injektiv und surjwktiv fragt hingegen:
gibts zu jedem bild <=1 urbild, mind. ein urbild oder genau ein urbild?
Nein denn eine Funktion geht unendlich lang bis zu den y werten