Wie berechnet man diese quadratische Funktion?
Aus quadratischen Platten mit der Seitenlänge x(in dm) werden durch Herausschneiden von Quadraten der Seitenlänge 2dm an den Ecken offene Kartons mit dem Volumen(in dm3) hergestellt. A) Stelle die Funtionsgleichung für die Funktion x-- V auf , zeichne den Graphen. B) Welches Volumen erhält man bei einer Seitenlänge von x=50cm bzw. x=2m?
6 Antworten
V = 2dm • (x - 4dm)²
Funktion im Bild
falsches Bild!!
Weil die Seitenlänge des Quadrates x ist. Wenn an den vier Ecken jeweils ein Quadrat mit der Seitelänge 2dm herausgeschnitten wird, ist die Seitelänge des Kistenboden x-2•2dm = x-4dm und das Volumen Bodenfläche mal Höhe. V = (x-4dm)² • x
Und was wäre ,wenn man für das x ,50 einsetzt?
V = (50dm - 4dm)² • 2dm = (46dm)² • 2 dm = 4.232 dm³ = 4,235 m³
Hm, hier ist etwas räumliche Vorstellung nötig bzw. eine gute Skizze.
Der Teil in der Mitte hat die Seitenlängen x-2*2dm=x-4dm und damit den Flächeninhalt (x-4dm)^2.
Die Höhe eines Kartons entspricht gerade der Länge eines Eckquadrats, das herausgeschnitten wurde, also 2 dm.
Demnach ist das Volumen eines Kartons gleich Grundfläche mal Höhe, also
(x-4dm)^2*2dm
bzw. wenn man Einheiten weglässt, einfach
V(x)=(x-4)^2*2=2*(x-4)^2
Ergibt dir irgendeeine gestreckte und verschobene Normalparabel.
Zeichnen überlass ich dir.
Bei b musst du einfach die x Werte einsetzen und kriegst das zugehörige Volumen.
So beiläufig: Mach dir klar dass aus praktischen Gründen nur x-Werte mit x>2dm realistisch sind.
und wenn dir langweilig ist und du ableiten kannst, hier eine ähnliche, aber doch andere Aufgabe:
Dieses Mal ist die Länge des grossen Quadrates fest (=5 dm), allerdings ist die Länge der 4 herausgestanzten Quadrate variabel, also gleich x.
bestimme V(x) und bestimme, für welchen Wert von x das Volumen des Kartons maximal ist.
Seitenlänge: x in dm (x>4 dm)
Es werden an allen vier Ecken Quadrate mit 2 dm Seitenlänge weggeschnitten.
Dazu macht man sich idealerweise eine Skizze (siehe Bild)
Für das Volumen der quadratischen Säule relevant sind:
die Höhe und die Grundfläche.
Die Höhe ist fest bei 2dm.
h = 2
Die Grundfläche hat den Flächeninhalt
G = (x-4)²
Für das Volumen gilt wegen V = Grundfläche * Höhe also
V = (x-4)² *2
V(x) = 2x² -16x + 32



zu b)
V(x) = 2x² -16x + 32
Es ist wichtig, die Einheiten anzupassen. V(x) ist für Dezimeter.
x1 = 50 cm = 5 dm
x2 = 2 m = 20 dm
V(5) = 2*5² -16*5 + 32 = 2 dm³
V(20) = ...

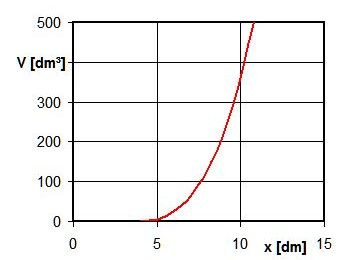
Habe hier nochmals den Graphen eingefügt, nachdem es beim a-Teil nicht geklappt hat.
So wie ich das verstanden habe:
f(V) = x³
Das Volumen ergibt sich aus einer variablen Kantenlänge.
oder
f(V) = (x + 2dm)³
+2dm wegen den Hervorstehenden Kanten
Wenn von Volumen die Rede ist, muss da unbedingt etwas mit x³ vorkommen.
höche*breite*tiefe, da sie aber bei einem Quadar alle gleich sind, ergibt sich sowas wie höche*höche*höche oder x*x*x oder x³. Die 2dm sind eine feste Größe für die Kantenlänge. Also ergibt x+2dm die Kantenlänge.
Falsch, es muss dm³ herauskommen, es kommt aber bei dieser Aufgabe kein x³ vor, weil die Höhe unabhängig von x ist.
Wieso steht in der Klammer (x - 4dm)