Graph fällt uns steigt?
Wir schreiben eine Mathe Arbeit und haben gerade quadratische Funktionen. Jetzt steht in der Aufgabe ,, In welchem Bereich fällt der Graph, in welchem steigt er? " kann mir dazu jemand was sagen?
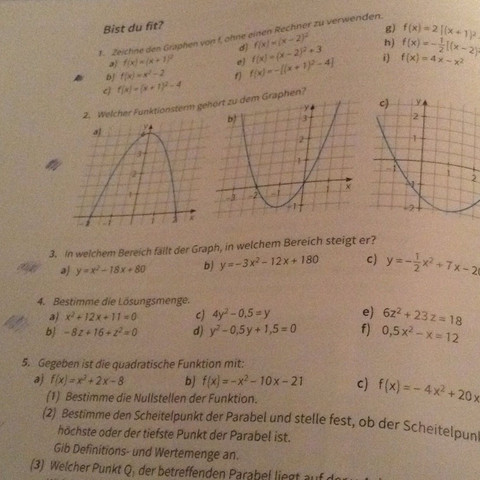
Ein Bild von der Aufgabe ist beigefügt:
Ich hätte gerne a.) einmal mit Lösungsweg und erklärt;) Danke im Vorraus ;)
2 Antworten
du bringst die gegebenen Gleichungen erst mal auf die Scheitelpunktform (mit quadratischer Ergänzung).. wenn du den Scheitelpunkt hast und durch das Vorzeichen weißt, ob die Parabel nach oben oder nach unten geöffnet ist, kannst du die Bereiche ganz einfach herleiten..
z.B. Scheitelpunkt bei (0/0) und nach oben geöffnet --> fallend von -unendlich bis (0/0) und steigend ab (0/0) bis + unendlich
zur Not machst du dir einfach eine kleine Zeichnung dazu, wenn du es dir nicht vorstellen kannst
Du musst erstmal in die Scheitelpunktform umwandeln, also
y=x^2 -18x+80
y=(x-9)^2 -1
Dann weißt du, dass der Scheitelpunkt der Parabel bei (9|-1) liegt und dann steigt sie im Bereich nach dem Scheitelpunkt und fällt in dem Bereich vorher.
Korrektur:
fallend: von minus unendlich bis 9 → ]-∞; 9]
steigend: von 9 bis unendlich → [9; ∞[
Das heißt fällt von unendlich bis (9/-1) und steigt von (9/-1)????