Wie berechne ich den Flächeninhalt eines Rechtecks unter einer Kurve ohne Integral?
In den beigefügten Bilder ist die Aufgabe enthalten, die ich lösen muss! Wie kann ich die erste Aufgabe lösen? Die zweite kann ich lösen indem ich den extremwert von der Funktion in a Bereiche, richtig?

4 Antworten
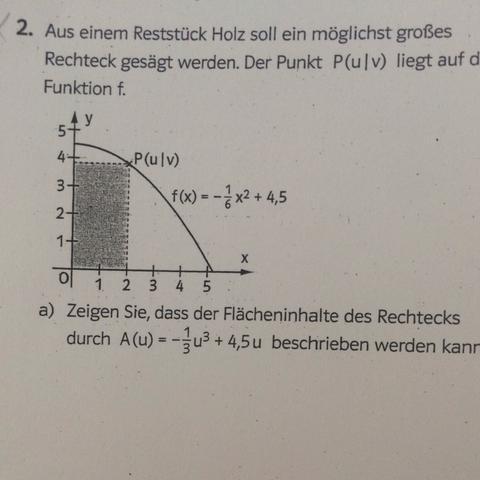
Eine Seite des Rechtecks geht von Null bis u, sie ist also u-0=u lang. Die zweite Seite geht von Null bis v, sie ist also v-0=v lang.
Das Rechteck hat also die Fläche A = u·v
Das der Punkt P(u|v) auf dem Graphen der Funktion f(x) liegt, gilt außerdem v = f(u) = -1/6u² +4,5
Damit gilt:
A = u·v = u·(-1/6u² +4,5) = -1/6u³ +4,5u
Und da A von u abhängt schreibt man eben:
A(u) = -1/6u³ +4,5u
Zu b) hast du absolut recht, das ist eine Extremwertaufgabe.
Die Antwort ist sehr hilfreich, allerdings muss ich ja beweisen, dass -1/3 u^3+4,5 u herauskommen, während die Lösung bei dir -1/6u^3 + 4,5u ist
mit u = x und v = y
f(u) = -1/6 * u² + 4,5
A(u) = u * f(u) = -1/6 * u³ +4,5 * u
(das -1/3 ist falsch !)
A'(u) = dA/du = -1/2 * u² + 4,5
Maximum für A bei A' = 0
u² = 9 >> u = 3 und v = 3
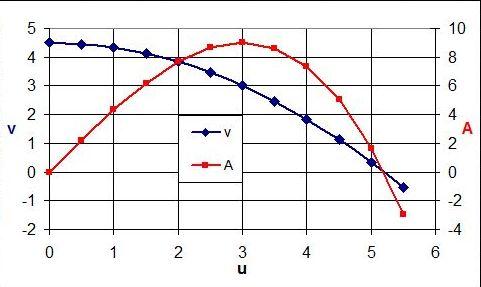
Siehe auch Bild: v(u) und A(u)
naja, flächeninhalt ist
A=x*f(x)=x*(-1/6*x^2+4,5)
das soll maximal werden, also machst du die üblichen Schritte bei ner Extremwertaufgabe :-)
A = u * (-1/6 u² + 4,5) und Klammer lösen;
b) ableiten und gleich 0 setzen; u berechnen und in A einsetzen.