Wertemenge gebrochen rationale Funktionen?
ich brauche hilfe bei der 1.3. ich steh frag aufm schlauch. wie gebe ich die wertemenge an?

2 Antworten
wieso da nur : Wertemenge von f und nicht Gf steht , ist mir ein Rätsel
Aber Gf stammt aus Aufgabe 1.0
kann f(x) Null werden ? Ja
kann f(x) + oder - unendlich werden ? Ja
warum ?
der Zähler ist immer positiv
der Nenner wird gegen unend entweder + oder -
Wertebereich daher R ( dachte ich ) bis :
Aber Gf hat eine SCHIEFE Asymptote !
und alle y-Werte der Glg
y = 0.25x + 0.75
sind nicht im Wertebereich
Beipiel x = 4 y = 1.75
x = -4 y = -0.25
überprüfen
ist 1.75 bzw -0.25 Teil von Gf ?
Nein :
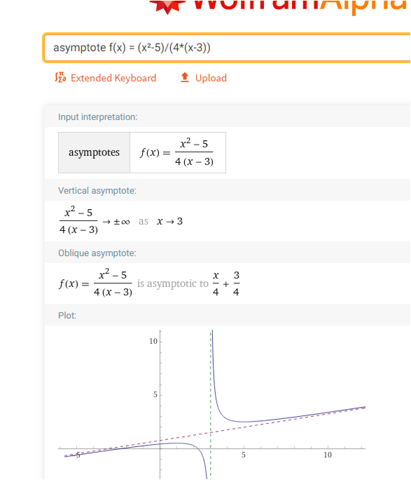
https://www.wolframalpha.com/input/?i=1.75++%3D+%28x%C2%B2-5%29%2F%284*%28x-3%29%29+
oder ist doch f' gemeint ?
nein , glaub ich nicht.
f(x) = (x²-5)/(4*(x-3))
g(x) = x/4 + 3/4
Unter Wertemenge verstehe ich alle möglichen Werte, welche die Funktion ausgeben kann.
Also z.B. die Funktion
ist zwar für jedes x definiert, aber es gibt z.B. kein x1 mit f(x1)=-1, also f(x)=-1 ist nicht Teil aller möglich Ergebnisse von f(x). Wenn du dieses f(x) weiter untersuchst, stellst du sicher fest, dass nur nicht-negative Werte angenommen werden. Also könnte man hier als Wertemenge W=[0,∞) angeben.
Also einfach die Menge aller möglichen Ergebnisse.
bei der gegebenen Fkt habe ich einen besonderen Wertebereich ermittelt . Kannst ja man Stellung dazu beziehen .
Für diese konkrete Funktion f. f’ wird für die Monotonieintervalle verwendet. Diese hat dann natürlich auch eine eigene (womöglich auch andere) Wertemenge.
Das stimmt so ja nicht. Der Wertebereich ist ja alles, auf was die Funktion prinzipiell abbilden kann. Setzt du in diese Geradengleichung aber x=17 ein, so folgt y=5, was laut deiner Aussage nicht im Wertebereich liegt, aber laut dem Graph oben, bildet die Funktion sehr wohl auf 5 ab.
Es ist vielleicht besser erstmal die Umkehrfunktion zu bestimmen:
f(x) = (x²-5)/(4*(x-3))
4*(x-3)*y=x^2-5
x^2 - 4y*x + 12y -5 = 0
p-q Formel: x = 2y +/- wurzel(4y^2 - 12y + 5)
Jetzt muss man nur noch Prüfen für welche Werte von y es einen x wert gibt. Das ist genau dann der Fall, falls 4y^2 - 12y + 5 >= 0 gilt, da dann die Wurzel definiert ist. Da dies eine nach oben geöffnete Parabel darstellt, muss man hier nur noch die Nullstellen rausbekommen:
y = 1,5 +/- wurzel(2,25 - 1,25) = 1,5 +/- 1
Die Nullstellen liegen also bei y = 0,5 und y = 2,5
Das bedeutet, dass es nur x Werte gibt für die Funktion mit Werten im Bereich
[-unendlich, 0,5] und [2.5 , unendlich] gibt. Und genau das ist dann also der Wertebereich