Wer hat Recht - ich oder mein Lehrer (Physik, Induktionsspannung)?
Hallo!
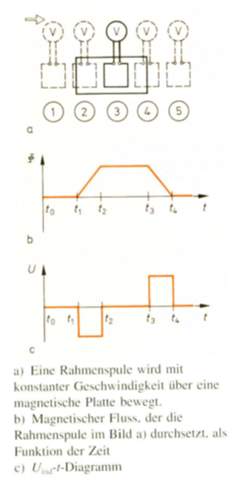
Ich habe in Physik ein paar Differenzen mit meinem Lehrer bezüglich einer Aufgabe (Grafik siehe Anhang). Sie lautet:
"Beschreiben Sie die aufeinander folgend auftretenden Induktionsspannungen, wenn sich die Rahmenspule im Bild zunächst der Magnetfläche nähert, sie dann mehr und mehr bedeckt und schließlich wieder von ihr herabgleitet! Erklären Sie die Effekte auf der Grundlage der Gleichung U ind = -N * A * dB/dt !"
Also: Diese Gleichung besagt doch, dass A konstant ist und B sich mit fortschreitendem t ändert (da B lt. Gleichung von t abhänhig ist). Meiner Auffassung nach muss man aber B konstant lassen und A mit laufendem t ändern, denn ich habe es so verstanden:
- A: Die vim Magnetfeld durchsetzte Fläche der Leiterspule
- B: Feldstärke der Platte
Macht auch Sinn, da man ja die Rahmenspule über das Ding bewegt und genau dann eine Spannung induziert wird, wenn die Leiterspule in das Magnetfeld eintritt, bis die Spule ganz drin ist (und das Gleiche natürlich auch, wenn sie wieder von dieser herabgleitet).
Mein Lehrer ist entgegen meiner Meinung (und der Meinung des Kurses) der Ansicht, dass A die Fläche der Magnetplatte sei. Nun stellt sich die Frage: Warum ändert sich B? Meine einzig logische Erklärung wäre folgende: Wenn ein Strom durch die Leiterschleife fließt, entsteht um den Draht ein ringförmiges Magnetfeld (also in "Ringen um den Draht"). Dieses verstärkt eventuell das B-Feld der Magnetplatte.
Allerdings ist das Problem, dass auch bei einem offenen Stromkreis eine Spannung beim Ein- und Austreten der Schleife in dieses Feld zu messen ist.
Wer liegt richtig - ich oder mein Lehrer? Wen ich richtig liege: Wie kann ich ihn davon überzeugen? Ich habe mir ernsthaft Mühe gemacht, das zu verstehen und ich bin nun komplett irritiert. Das macht mich ziemlich sauer, um ehrlich zu sein.
Danke für eure Mühe und einen schönen Abend noch!
LG
3 Antworten
Du brauchst nicht sauer zu sein, du hast wahrscheinlich unbewusst die Gemeinheit des Induktionsgesetzes entdeckt, die in der Schule oft verschwiegen wird (aus didaktischen Gründen).
Die Erklärung der induzierten Spannung gelingt nämlich nur in einem Bezugssystem mit dem Induktionsgesetz, im anderen Bezugssystem braucht man die Lorentzkraft.
Du hast die Aufgabe so verstanden, dass die Leiterschleife über das Magnetfeld gleitet, so ist die Aufgabe ja auch formuliert. Insofern hast du also recht, das Magnetfeld ist konstant. Dummerweise liefert in diesem Bezugssystem (nämlich das des ruhenden Magneten) das Induktionsgesetz keine Induktionsspannung, denn durch das ruhende Magnetfeld ändert sich auch der Magnetische Fluss nicht, also d(A * B) = 0.
Grund für die Induktionsspannung ist die Lorentzkraft. In den Leiterstücken senkrecht zur Bewegungsrichtung gibt es in beiden Stücken eine Lorentzkraft, welche den Strom in der Leiterschleife antreibt. FC = Q * (v x B). Damit lässt sich der korrekte Wert für den Strom bzw. die Spannung ermitteln.
Nun das Bezugssystem Schleife: Hier ruht die Schleife und die magnetische Platte bewegt sich (in die andere Richtung wie oben). Hier ändert sich der magnetische Fluss, und zwar durch dB/dt, denn das Magnetfeld bewegt sich. Die Fläche bleibt konstant, sie bewegt sich ja nicht. Damit ist die von deinem Lehrer angegebene Gleichung korrekt.
Aber: Man muss beim Angeben dieser Gleichung schon sagen, in welchem Bezugssystem man sich befindet, sonst gerät man in Schwierigkeiten, zumindest dann, wenn Schüler anfangen nachzudenken :-)
Hoffe, ich konnte helfen, und bitte immer weiter nachdenken.
Aus der Sicht der ruhenden Leiterschleife bewegt sich der Magnet über die Leiterschleife. Der magnetische Fluss ist ja phi = A * B. Damit gilt nach der Produktregel dphi = A * dB + B * dA.
Die Fläche der Leiterschleife ändert sich aber nicht, daher dA = 0, also bleibt dphi = A * dB. Da das Magnetfeld über das ruhende System wandert, ändert sich die Struktur der Magnetfeldlinien, also ist auch dB <> 0, damit hast du auch die Induktionsspannung gemäß der Formel von oben.
Nun zur Lorentzkraft: Hier muss man aufpassen. In der Schule hat man meistens nur FL = Q * (v x B). Wegen der ruhenden Spule wäre hier v = 0 und damit FL = 0, obwohl B <> 0 ist. Du hättest hier also keine Kraft auf die Ladungen Q und damit auch keinen Strom. Man sieht also, dass diese Formel für die Lorentzkraft nur die halbe Wahrheit erzählt, es ist nämlich die mathematische Beschreibung der Kraft aus der Sicht des ruhenden Magnetfelds (Hier ist nämlich v <> 0). Der korrekte und vollständige Term lautet auch daher
FL = Q * (E + v x B).
Wegen v = 0 (aus der Sicht der ruhenen Leiterschleife) ist hier nur
FL = Q * E.
Wo kommt nun dieses elektrische Feld E her? Nun, dies wird eben durch die Induktionsformel von oben beschreiben, in der Spule wird also ein elektrisches Wirbelfeld induziert, und dieses treibt den Strom an.
Fazit: Aus der Sicht des ruhenden Magneten wird der elektrische Strom durch den Term v x B in Gang gesetzt, weil sich die Ladungsträger mit v bewegen. Aus der Sicht der ruhenden Leiterschleife wird der Strom durch das elektrische Wirbelfeld E in Gang gesetzt, welches mit dem Induktionsgesetz beschrieben wird.
Vielen vielen Dank, du hast mir unglaublich geholfen! Mein Lehrer findet es übrigens super, dass ich das so hinterfrage und wenn wir ein Stückchen weiter sind, möchte er mir das nochmal genauer erklären.
Ihr habt beide in gewisser Weise recht. Es ist der Blickpunkt entscheidend.
Sichtweise 1 (so wird es normalerweise gemacht und der Lehrer hätte Recht)
B ist die Flussänderung in der Spule, nicht dem homogenen Magnetfeld des Erzeugers.
B=0 wenn die Spule außerhalb des homogenen Feldes ist.
Die fläche A sei die Fläche der Spule, welche natürlich konstant ist, da du die Spule nicht zusammendrückst etc.
Sichtweise 2 (untypisch, du hättest recht)
B sei der Fluss des Erzeugers, welcher ein homogenes Magnetfeld aufbaut. Er sei konstant.
A sei die von Magnetfeld durchsetzte Änderung der Fläche der spule. Diese ändert sich, wenn sich die Spule in das Feld bewegt.
Da die Induktionsgleichung so aufgestellt worden ist, dass A konstant und B von t abhängig ist, hat in diesem Zusammenhang also dein Lehrer recht.
Man könnte die Formel auch anders notieren, wird in der Praxis jedoch zur Vereinheitlichung nicht gemacht.
Die Sichtweise 2 ist so aber nur die halbe Wahrheit. Zwar ist hier dphi = A * dB + B * dA = B * dA wegen dB = 0, daher liefert das Induktionsgesetz auch ein elektrisches Wirbelfeld, damit hast du aber nicht die komplette Induktionsspannung. Das komplette in der LEiterschleife erzeugte elektrische Feld Ekomplett beträgt nach der Lorentzkraft
Ekomplett = E + v x B, mit dem Induktionsgesetz bekommst du aber nur den Term E, nicht aber den Term v x B, die reine Anwendung des Induktionsgesetzes liefert also einen falschen Wert, du hast hier eine schwierige Berechnung, nämlich einen Teil Induktionsgesetz und einen Teil von v und B abhängige Lorentzkraft. Um diese mathematische Schwierigkeit zu umgehen, nimmt man ein einfacheres Bezugssystem, nämlich das der Leiterschleife, und hier ist nämlich v = 0 und dA = 0, also nur dphi = A * dB.
Das ist das, was der Lehrer meint, allerdings muss einem klar sein, dass die geeignete Wahl des Bezugssystems ein mathematisch geschickter Zug ist, aber keine physikalische Notwendigkeit.
Danke! Ich bin von meinem Standpunkt aufgrund der Aufgabenformulierung ausgegangen.
Ich sehe in dem Kreis mit dem "V" ein Voltmeter, also ein Spannungsmessgerät, aber mit Sicherheit keine Spannungsquelle. Von daher erzeugt die Leiterschleife kein elektrisches Feld, sondern wandelt ein veränderliches Magnetfeld in eine Spannung um.
Veränderlich ist dieses Magnetfeld aber nur, wenn sich ein Magnet relativ zur Leiterschleife bewegt.
Leider ist nicht zu erkennen, wie die Pole der Magnetplatte ausgerichtet sind. Würde das Magnetfeld von rechts nach links gehen, würde vermutlich die Leiterschleife während des gesamten Transits der Magnetplatte eine Spannung erzeugen. Ist jedoch das Magnetfeld von oben nach unten ausgerichtet oder durch die Spule hindurch wird vermutlich nur eine Spannung in der Leiterschleife erzeugt, wenn das Magnetfeld in die Leiterschleife (von der Fläche innerhalb der Leiterschleife gesehen) eindringt, bzw. diese verlässt.
B zeigt die Stärke des magnetischen Feldes an, während das Magnetfeld sich auf die Leiterschleife auswirkt. Während das Magnetfeld in die Leiterschleife eintritt, wird die Stärke des Magnetfeldes größer und beim Verlassen wird sie geringer.
C zeigt schließlich an, dass nur dann eine Spannung erzeugt wird, wenn das Magnetfeld sich verändert, was ein ähnliches Prinzip ist, wie beim Trafo denn auch dieser kann nur Wechselspannungen transformieren, weil er dazu ein veränderliches elektrisches Feld benötigt (ebenso ist es übrigens auch bei einem Generator)
Fazit: Der Lehrer hat recht. Aber vielleicht hilft Dir meine Antwort oder eventuell eine andere Antwort, die Aufgabe besser zu verstehen.
Vielen lieben Dank für die Antwort! Ich kann nur nicht nachvollziehen, warum sich der magnetische Fluss ändert, wenn sich das Magnetfeld bewegt. Das macht für mich logisch gerade keinen Sinn, sorry.
Ich werde aich weiter nachdenken, ich hinterfrage so gut wie alles. Nett, wie er uns das verschweigt. Sonst ist er doch so penibel, dann bitte auch bei solchen Aufgaben...ich versuche mal weiter, das nachzivollziehen. Das mot dee Lorentzkraft war mir schon davor klar. Und ich dachte, ich hätte das Thema voll gut durchblickt :(