Warum ist das Vorgehen nicht egal?
Hallo zusammen,
ich habe eine Frage, die ich als sehr wichtig empfinde. Und zwar wurde mir mitgeteilt, dass das Vorgehen beim Zeichnen einer Parabel man bestimmte Sachen nicht vertauschen kann, ich verstehe das aber irgendwie nicht ganz.
Beispiel : Um 2 Einheiten nach oben verschieben und dann an der x-Achse spiegeln, ist nicht dasselbe wie zuerst spiegeln und danach nach oben um 2 Einheiten verschieben. Der Scheitelpunkt verändert sich meiner Meinung nach nicht oder liege ich falsch?
Hoffe schnellstmöglich auf eine ausführliche und gute Antwort.
Danke im Vorraus!
3 Antworten
Hallo Alice,
lass uns schauen!
Um 2 nach oben verschieben geht so: f(x) -> g(x)=f(x)+2
An der x-Achse spiegeln geht so: f(x) -> g(x)=-f(x)
Wir starten mit f(x)=x².
Um 2 nach oben verschoben erhalten wir f(x)=x² -> g(x)=x²+2
An der x-Achse gespiegelt erhalten wir g(x)=x²+2 -> h(x)=-(x²+2)=-x²-2
Jetzt umgekehrt! Wieder f(x)=x².
An der x-Achse gespiegelt erhalten wir f(x)=x² -> g(x)=-x²
Um 2 nach oben verschoben erhalten wir g(x)=-x² -> h(x)=-x²+2
Also, Tatsache, ist eine andere Funktion!
Doch. Sei der Scheitelpunkt zB bei (0/0)
Erst zwei nach oben: (0/2)
Dann spiegeln: (0/-2)
Und andersrum
Erst spiegeln: (0/0)
Dann zwei nach oben: (0/2)
Und (0/-2) ist nicht das gleiche wie (0/2)
Ein kleines Experiment...
- Startposition: Stelle dich an einen gewissen Punkt und blicke in eine gewisse Richtung.
- Gehe zwei Schritte nach vorne und drehe dich dann um (um 180°). Merke dir die Stelle.
- Nehme wieder die Startposition (mit Startrichtung) ein.
- Drehe dich um (um 180°) und gehe zwei Schritte nach vorne. Bist du nun an der gleichen Stelle, die du dir gemerkt hattest? Nein, bist du nicht.
Es kommt hier also darauf an, ob du dich zuerst umdrehst und dann läufst, oder ob du zuerst läufst und dich dann umdrehst.
============
1. Situation...
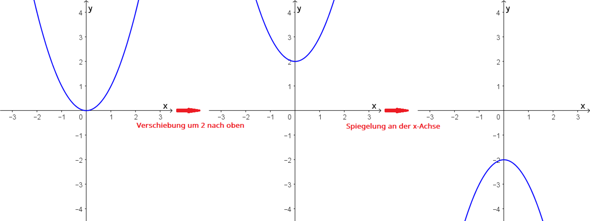
f₁(x) = x² --> f₂(x) = x² + 2 --> f₃(x) = -(x² + 2) = -x² - 2
------------
2. Situation...

f₁(x) = x² --> f₂(x) = -x² --> f₃(x) = -x² + 2
------------
Und? Ist der Scheitelpunkt der Parabel am Ende in beiden Situationen an der gleichen Stelle? Nein.


Ich dachte, dass wenn ich eine Parabel spiegele, der Scheitelpunkt sich nicht verändert.