Vollständige Induktion?
Hallo zusammen,
kann mir bitte jemand bei folgender Aufgabe helfen. Es soll mit vollständiger Induktion bewiesen werden.
Für alle nEN gilt: n/6+n^2/2+n^3/3 EN
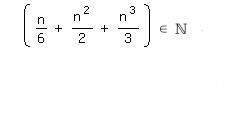
Ich freue mich über die Antworten.
Vielen Dank im voraus.
2 Antworten
Willy hat dir den Beweis ja schon skizziert, und du sollst das ja auch per vollständiger Induktion machen. Sinnvoll ist das hier allerdings nicht, weil das auch direkt geht.
Es ist
Um zu zeigen, dass das eine natürliche Zahl ist, muss man zeigen, dass der Zähler durch 6 teilbar ist. Nun kann ich fröhlich umformen:
n + 3n² + 2n³ = n[1+3n+2n²] (n ausgeklammert)
= n[1 + 2n + n + n² + n²] (nix passiert, nur auseinandergezogen)
= n [ 1+ 2n + n² + n + n²] (umsortiert)
= n [(1+n)² + n + n²] (binomische Formel)
= n [(1+n)² + n(1+n)] (n ausgeklammert)
= n [ (1+n) ((1+n) +n) ] ((1+n) ausgeklammert)
= n [ (1+n) (2n + 1)] (zusammengefasst)
= n (n+1) (2n+1) (überflüssige Klammer weg)
Eine Zahl ist durch 6 teilbar, wenn sie durch 2 und durch 3 teilbar ist. Schauen wir uns das Produkt bzw. die einzelnen Faktoren an, so kann man folgendes sagen:
Auf jeden Fall ist einer der beiden Faktoren n und n+1 durch 2 teilbar, da von zwei aufeinanderfolgenden Zahlen immer eine gerade ist. Also ist das Produkt durch 2 teilbar.
Wenn n oder n+1 durch 3 teilbar ist, sind wir fertig, denn dann ist das Produkt auch durch 3 teilbar. Wenn nun weder n noch n+1 durch 3 teilbar sind, dann sind sowohl n-1 also auch n+2 durch 3 teilbar, denn von drei aufeinander folgenden Zahlen ist immer eine durch 3 teilbar, also ist von n-1, n, n+1 eine Zahl durch drei teilbar und von n, n+1, n+2 auch. Da wir ausgeschlossen haben, dass n oder n+1 durch 3 teilbar ist, müssen eben n-1 und n+2 durch 3 teilbar sein. Dann ist aber auch die Summe aus beiden, nämlich (n-1) + (n+2) durch 3 teilbar. Es ist aber gerade
(n-1) + (n+2) = 2n + 1
und das ist gerade unser dritter Faktor. Damit haben wir gezeigt, dass auf jeden Fall einer der drei Faktoren unseres Produkts durch drei teilbar ist, und sind insgesamt fertig.
Hallo,
das ist die bekannte Summenformel für die Summe von k² für k=1 bis k=n.
Beweise einfach diese Summenformel, dann verschwinden die Brüche automatisch.
Herzliche Grüße,
Willy
Du kannst es natürlich auch beweisen, indem Du statt n den Term (n+1) einsetzt und davon n³/3+n²/2+n/6, der ja laut Voraussetzung Element der natürlichen Zahlen ist, abziehst. Natürlich vorher alles gleichnamig machen, also alles auf Sechstel. Aus dem Restterm läßt sich die 6 kürzen, so daß keine Brüche mehr vorhanden sind.
Mit meiner Methode schlägst Du allerdings zwei Fliegen mit einer Klappe, weil Du die Summenformel en passant mitbeweist.