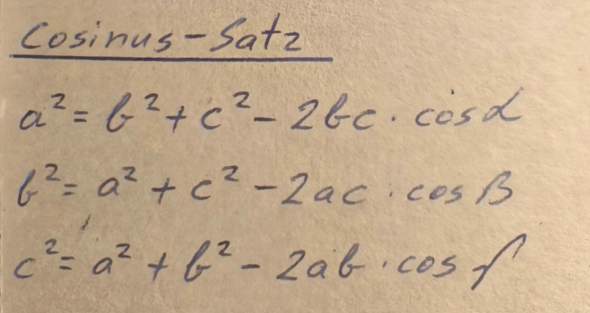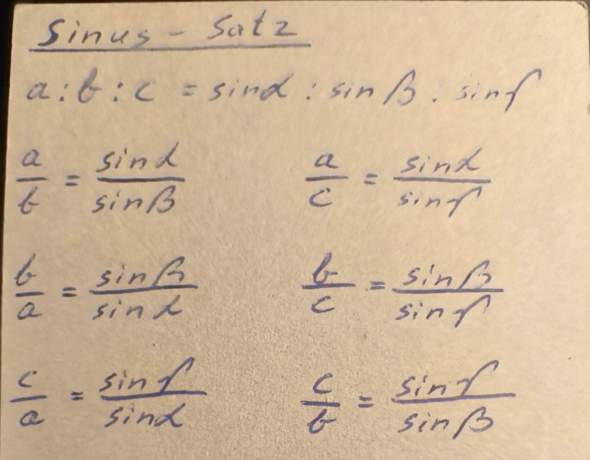Wie funktioniert Sinus, cosinus, Tanges mit sdp?

Ich hab ein Blatt bekommen heißt wenn ich es mache kriege ich eine gute Note zählt als Test aber ich versteh nicht wie es genau funktioniert und da steht gib den lösungsplan ist ohne zahlen weil mir nur so Buchstaben gegeben sind oder
theman : sinus, cosinus, Tanges (hab schon bissl begonnen)
1 Antwort
Bei Figur 1 musst du mit dem Cosinussatz die dritte Seite berechnen. Da dir a, b und Gamma gegeben sind, also ...
c^2 = a^2 + b^2 - 2*a*b*cos(Gamma) bzw. dann natürlich die Wurzel ziehen.
Die Höhe ha kannst du nicht mit Pythagoras berechnen. Richtig ist ha = b* sin(Gamma). Aber da du nur c berechnen sollst, brauchst du ha nicht.
Hier noch eine kleine Hilfe zu dem Cosinussatz

Bei Figur 2 hast du ein rechtwinkliges Dreieck und kannst b (ist hier die Hypotenuse) mit den "normalen" Winkelfunktionen berechnen. Dazu diese Merkhilfe

GK= Gegenkatheter Ak= Ankathete und Hyp= Hypotenuse
Bei Figur 3 hast du wieder ein schiefwinkliges Dreieck und musst aber mit dem Sinussatz rechnen. Dazu diese Merkhilfe

Zuerst mit a/b = sin(a)/sin(ß) den Winkel ß berechnen und dann kannst du mit dem gegebenen und dem berechneten auch den Winkel Gamma berechnen.
Bei Figur 4 musst du c über die Berechnung der zwei Teilstücke berechnen. Ich nenne hier D den Punkt auf dem hc senkrecht auf c steht. Das Teilstück von A nach D mit Pythagoras berechnen (b ist die Hypotenuse und hc eine der Katheten). Das Teilstück von D nach B mit dem Tangens berechnen. Mittlere Merkhilfe nutzen. Beide Teilstücke addieren und du hast c.