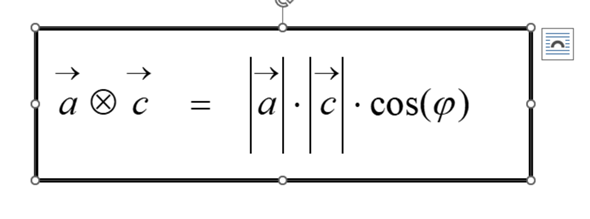
Unser thema ist momentan skalarprodukte und ich verstehe diese aufgabe nicht bitte lösung mit erklärung zu dieser aufgabe?

3 Antworten
Ich sehe den Zusammenhang mit Skalarprodukt nicht, aber mir scheint die Lösung recht schlicht. Vektor V ist offensichtlich die "Quadrantendiagonale".
(als Funktion f(x) = x).
45° muss also eine der Achsen sein, und damit kommt nur a= 0 in Frage
Für den Winkel w zwischen zwei Vektoren u und v gilt:
cos(w) = u*v/( |u| * |v| )
Die Aufgabe hat deshalb mit dem Skalarprodukt zu tun, weil das im Zähler des Bruches steht.
cos(w) = (4 + a)/( |sqrt(4² + a²)| * |sqrt(2)| )
Wegen cos(45°) = 1/sqrt(2):
1/sqrt(2) = (4 + a)/( sqrt(4² + a²) * sqrt(2) )
1 = (4 + a) / sqrt(4² + a²)
sqrt(4² + a²) = 4 + a
Diese Gleichung gilt nur für a = 0.
Hinweis:

Dieser Ansatz führt zu einer Gleichung mit einer Wurzel, die dann durch Quadrieren zu einer quadratischen Gleichung gemacht werden kann..