Umkehrfunktion von cosh(x) bilden?

Wie bilde ich die Umkehrfunktion dieser Funktion:

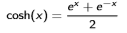
Danke :)

Answer 1

[mihisu]

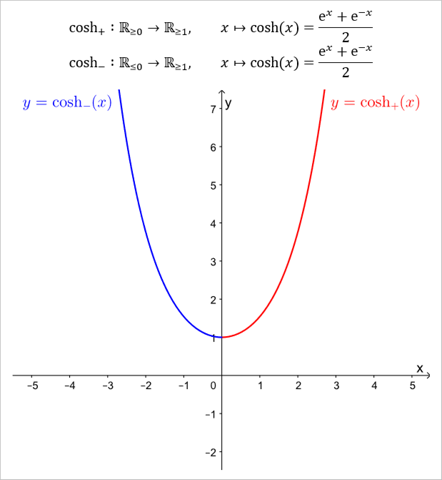
Die cosh-Funktion ist nicht umkehrbar (d.h. nicht bijektiv), da sie nicht injektiv ist. Beispielsweise ist cosh(1) = cosh(-1), obwohl 1 ≠ -1 ist. Man kann jedoch beispielsweise die folgenden beiden Einschränkungen umkehren...

============

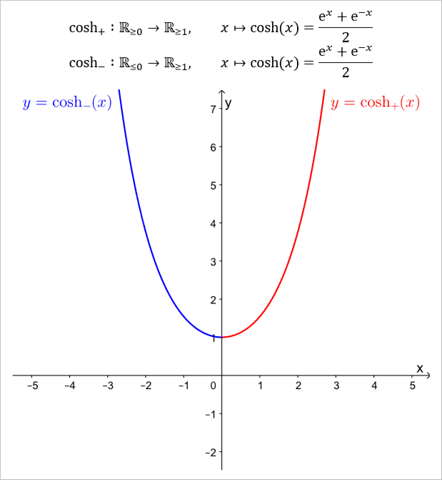
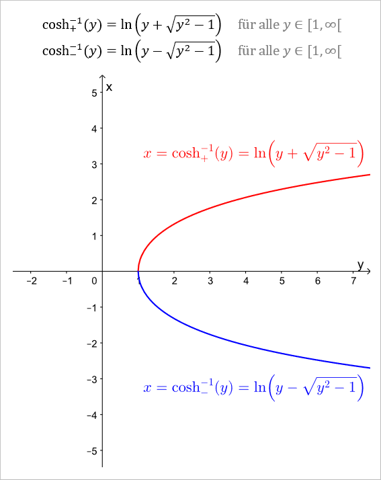
Um eine Gleichung der Umkehrfunktion zu erhalten kann man vorgehen, wie sonst meistens auch bei der Bestimmung der Umkehrfunktion. Löse die Funktionsgleichung nach x auf. Also löse die Gleichung...

$y=\frac{\text{e}^x+\text{e}^{-x}}{2}$

... nach x auf.

Damit erhält man also...

============

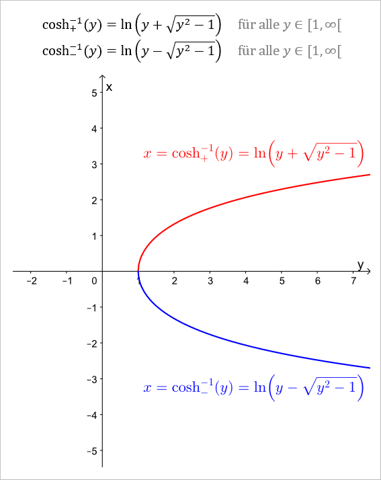
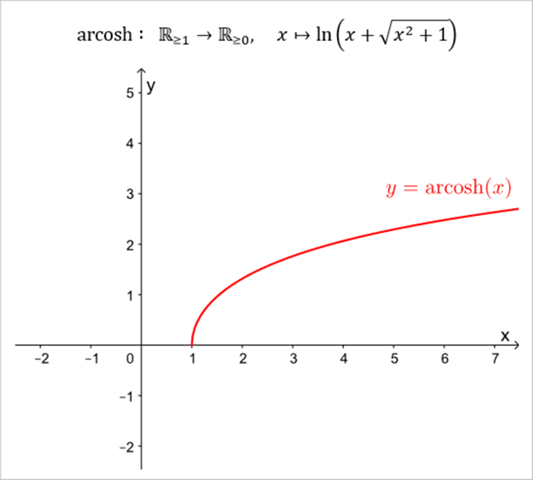
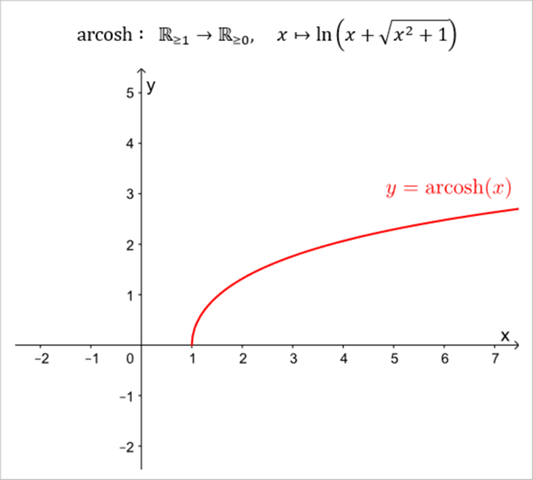
Die Umkehrfunktion der Einschränkung cosh₊ bezeichnet man übrigens als Areakosinus hyperbolicus.

https://de.wikipedia.org/wiki/Areasinus_hyperbolicus_und_Areakosinus_hyperbolicus

Answer 2

[Applwind]

$x=\frac{e^y+e^{-y}}{2}\Leftrightarrow2x=e^y+e^{-y}\Leftrightarrow e^y+e^{-y}-2x=0$

Alles *e^y und dann Substituieren.

Achtung : Du darfst später nur einen Zweig wählen, für die Umkehrfunktion.

Woher ich das weiß: Hobby – Schüler.

Answer 3

[Tiger978]

setze die funktion gleich y und forme nach x um