Surjektiv, injektiv, bijektiv?

Können mehrere a auf b bzw b auf c abgebildet werden?

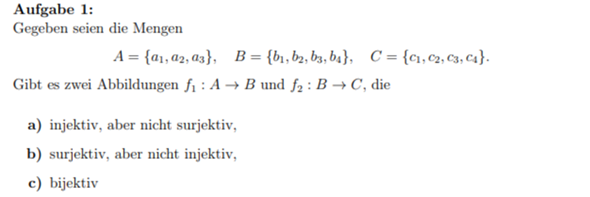
Wenn nein, müssten die ergebnisse doch so aussehen oder?


f1: {(a1,b1);(a2,b2);(a3,b3)}
f2: {(b1,c1);(b2,c2);(b3,c3);(b4,c4)}

b)
f1: funktioniert nicht
f2: funktioniert nicht
c)

f1: funktioniert nicht
f2: {(b1,c1);(b2,c2);(b3,c3);(b4,c4)}

Answer 1

[RitterToby08]

Können mehrere a auf b bzw b auf c abgebildet werden?

Wie ist das gemeint? Es müssen natürlich alle Elemente aus A nach B abgebildet werden, damit es eine Funktion ist. Nicht erlaubt ist jedoch z.B. folgende Zuordnung:

a1-->b1 und a1-->b2

Deine Funktionen sind alles wirklich Funktionen (wenn ich deine Schreibweise richtig verstehe). Aber korrekt ist die Aufgabe nicht ganz, denn bei a) ist f2 surjektiv.

Grundsätzlich gilt für Mengen X,Y mit |X|=|Y| und f:X-->Y eine Abbildung, dass injektiv, surjektiv und bijektiv äquivalent sind.

Comments

[mltzmlml]

danke!
wenn ich das richtig verstehe, geht a)f2 auch nicht oder?

[RitterToby08]

@mltzmlml

Genau, denn:

Grundsätzlich gilt für Mengen X,Y mit |X|=|Y| und f:X-->Y eine Abbildung, dass injektiv, surjektiv und bijektiv äquivalent sind.

Answer 2

[diderot2019]

b) und c) ist korrekt. Bei a) f2 ist deine Abbildung surjektiv. Das dürfte sie nicht.