Streckung eines Graphen um Faktor 3 und Verschiebung um 2 Einheiten nach oben (Mathematik)?
Muss man bei der Streckung den ganzen Term mit 3 multiplizieren bsp.1 oder nur die Zahlen vor den xsen bsp.2?
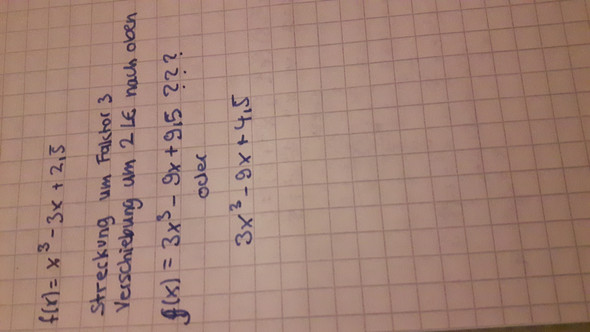
3 Antworten
Hallo partizipperfekt.
Zu deiner "Entwirrung" folgendes:
Rhenane hat Recht. Streckung heißt, dass jeder y-Wert, also jeder Wert von f(x) mit dem gleichen Faktor multipliziert werden muss. Bei dir ist es der Faktor 3, also heißt die gestreckte Funktion g(x) = 3*f(x) = 3*(x³ - 3x +2,5) = 3x³ - 9x + 7,5. Wenn diese Funktion noch zusätzlich um 2 nach oben verschoben werden soll. muss zu jedem Funktionswert noch 2 addiert werden. Damit erhält man schließlich v(x) = g(x) + 2 = 3x³ - 9x + 9,5, wie von dir bereits berechnet.
Es grüßt HEWKLDOe.
Bei der Streckung muss die gesamte Funktion mit dem Streckungsfaktor multipliziert werden, d. h.: g(x)=3 * f(x) = 3 * (x³-3x+2,5)
und dann noch +2 zum Verschieben in y-Richtung, also wie in Deinem 1. Beispiel.
Das ist immer so. Die Gerade ist beim Strecken dann einfach nur steiler bzw. beim Stauchen flacher. Das, was gleich bleibt ist die Nullstelle, wie bei allen anderen gestreckten/gestauchten Funktionen und deren "Urfunktion" auch. Ist ja auch logisch. Ist der y-Wert bei Einsetzen eines bestimmten x-Wertes Null, dann ist er es auch, wenn man den gesamten Term zusätzlich mit irgendeinem Faktor multipliziert.
der Kommentar unter dir behauptet aber etwas anderes
Strecken oder Stauchen kann man ja keine Gerade, also das lineare Glied und die Konstante ist die y-Verschiebung. Streckung also nur auf die nichtlinearen Glieder, hier nur bei x³!
das wird doch dann zu 6x-1 oder? Aber das ist linear...
Hast du schon mal eine gerade gestaucht? Da wird aus der Geraden eine krumme Kurve, also was vollkommen entgegen Gesetztes! Für Geraden gibr es keine Stauchung oder Streckung!
wenn da aber statt x auch x hoch 2 oder 4 oder sonstwas stehen würde?
Hab ich doch beschrieben,nur die nichtlinearen Glieder x², x³, x^4, x^5 ... aber nicht das lineare Glied x^1
gut zu wissen :) Ist das bei linearen Funktionen auch so?