Schiefe Ebene Kräfte?
Bsp: man schiebe einen Gegenstand auf der flachen Ebene, dabei wird Reibungsarbeit verrichtet. Schiebe ich nun selbigen Klotz die selbe Strecke aber eine schiefe Ebene hoch, so muss mehr Arbeit verrichtet werden weil der Körper am Ende auch noch potentielle Energie hat. In der schiefen ebene kann man ja die Gravitationskraft in hangabtriebskraft und normalkraft aufsplitten wobei die beiden letzteren genannten aber ja keine wirklichen Kräfte sind.
Meine Fragen:
1. wenn die beiden Kräfte ja keine „wirklich wirkenden“ Kräfte sind warum kann man dann damit rechnen?
2.durch die Höhe wird ja potentielle enegrie benötigt. Kann man diese potentielle Energie nun auch durch einen kraftpfeil in der schiefen Ebene darstellen oder welche Kraft muss man aufwenden zusätzlich zur Reibungskraft?
3. ist die Reibung in der schiefen ebene dieselbe wie in der Flachen Ebene denn im Internet stand die Reibung hängt von der normalkraft ab diese ist aber in der schiefen ebene ja betragsnässif kleiner .
Vielen Dank
3 Antworten
Zu 1:
Es gibt zwei Lehrmeinungen, wie man das den Lernenden beibringt.
Die erste, die du erwähnst (mit der "Zerlegung" der Gravitaitionskraft) finde ich verwirrend und nicht konsequent nach Newton, weil da unnötigerweise eine nach unten zeigende Normalkraft entsteht (die bei nicht-schiefer Ebene nach oben zeigt).
Bei der besseren Methode zeigt die Normalkraft nach oben, es ist die "Gegen"Kraft, welche die Unterlage gegen das Objekt ausübt, um es zu stützen! "Normal" heisst senkrecht von der Unterlage gegen das Objekt.
So bekommt man eine resultierende Kraft, wenn sich das Ding beschleunigt, und eine Kräftesumme von null, wenn das Objekt in Ruhe ist oder sich gleichmässig bewegt. Genau wie es sich bei Newton gehört.
Zu 2:
Energie kannst du nicht als Kraftpfeil darstellen. Kraft und Arbeit oder Kraft und Energie kann man nicht gleichsetzen.
Aber die Kräfte kannst du addieren, wenn sie in gleicher Richtung wirken. Wenn du das Ding den Hang hochziehst, musst du zusätzlich zur Reibungskraft noch die Hangabtriebskraft kompensieren, diese Pfeile und Kraftbeträge addieren sich.
Zu 3:
Genau, die Reibungskraft wird mit zunehmender Schieflage kleiner, weil die Normalkraft kleiner wird (dafür nimmt die Hangabtriebskraft zu).
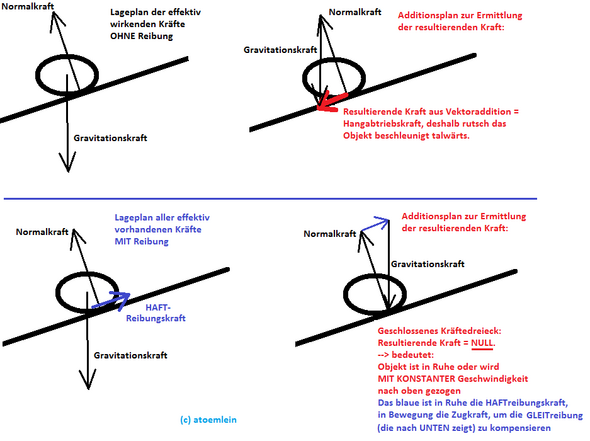
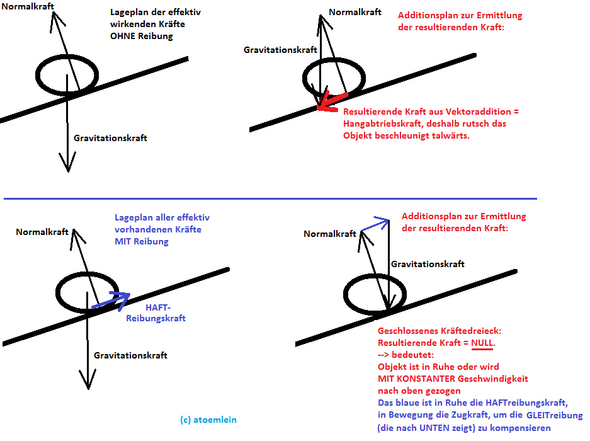
Die Zeichungen sollten sich einige Leute, vor allem Buchautoren von "deutschen" Physikbüchern, mal anschauen, so macht man eine physikalisch korrekte Kraftskizze. Interessanterweise sind im englischen Sprachraum die Kraftskizze in Büchern oder auch bei Wiki immer richtig
Ps: da wir hier ein wenig abgeschweift sind habe ich nochmal eine andere frage verfasst die sich auch mit der normalkraft und der schiefen ebene beschäftigt, aber nichts was du mir nicht schon gesagt hast.
Wie schon bei anderer Gelenheit erwähnt:
Wenn die Kraft senkrecht zum Weg ist, trägt sie physikalisch nichts zur Arbeit bei.
- Wenn eine Maschine den Schlitten schief zieht, braucht sie nicht mehr Energie, als wenn sie gerade zieht (siehe z.B. Skilift mit Tellern oder Bügeln)
- Für einen Menschen ist es halt eben trotzdem anstrengender, schief zu ziehen (oder eben eine Tasche zu halten, ohne sie zu bewegen), auch wenn da physikalisch keine Arbeit verrichtet und keine Energie benötigt wird.
Aber du sagtest ja die auflagenstärkste ist unabhängig von der Fläche die aufliegt müsste dann nicht so lange der Schlitten den Boden noch berührt die Kraft trz den gleichen Betrag haben wie gravitationskraft ?
Genau, Normalkraft und damit die Reibungskraft sind unabhängig von der Auflagefläche.
Aber wenn du den Schlitten schief ziehst, ändert sich ja die Auflagefläche der Kufen nicht. Du nimmst dem Schlitten aber etwas "Gewicht" weg, als ob eine Person weniger draufsitzen würde, damit sinkt die Last und damit die Normalkraft und somit auch die Reibungskraft.
Zu deinem Kommentar :
Warum rutscht eine Kugel ohne Reibung nur?
Zu den Kräften: habe es verstanden wie du erklärt hast. Habe auch nochmal in meinem Physik Buch nachgelesen (tipler kennst du sicher) da ist das mit der normalkraft auch so erklärt wie du es sagst. Da war auch ein Bild von einem Schlitten der gezogen wird auf Flachem Boden. Da war die gravitationskraft vom Betrag her gleich wie die normalkraft. Wird der Schlitten aber nicht parallel zu Boden gezogen sondern mit einem Winkel dazu so wie der Betrag der normalkraft kleiner
Wie kommt das?
Beide Themen wären fast neue Fragen wert, aber ich versuch's mal:
Die Nachfrage zur Kugel hab ich erwartet... Kurz:
- es gelten die Verhältnisse meiner Skizze oben rechts.
- Fg greift im Kugelzentrum an (Schwerpunkt)
- Normalkraft FN zeigt vom Auflagepunkt der Kugel senkrecht zur Unterlage nach oben durch das Kugelzentrum
- resultierende Kraft aus Fg und FN nach schief unten greift auch im Schwerpunkt an
- es kann also kein Drehmoment entstehen, das Ding dreht nicht, sondern rutscht nur (falls ohne Reibung)
Für die Verhältnisse mit Reibung muss man nun eben aufpassen bzw. genauer zeichnen:
- Die Reibungskraft greift unten am Auflagepunkt an und zeigt nach oben
- die resultierende Hangabtriebskraft greift im Schwerpunkt an
- so entsteht ein Drehmoment
Zum Schlitten:
Wenn du schief nach oben ziehst, "hebst" du den Schlitten ja leicht an (im Extremfall senkrecht), und damit reduziert sich die Reaktionskraft des Bodens, eben die Normalkraft und damit die Auflagekraft. Die Gravitationskraft wird dann kompensiert durch die senkrechte Komponente der Zugkraft und den Rest der Normalkraft).
Aber sind massepunkt und Schwerpunkt nicht das gleiche?
Des Weiteren erwähntest du, dass man ja bei dem Angriffspunkt der Kräfte aufpassen muss, ist das in der Zeichnung bei Wikipedia auch so weil die normalkraft da ja irgendwie aus dem Zentrum der schiefen ebene nach oben geht
Fast das gleiche.
- Massepunkt ist etwas Gedachtes, man schrumpft den Körper zu einem Punkt
- Schwerpunkt ist der reale Massenmittelpunkt, wo die Gravitationskraft "angreift", wenn der Stein frei hängt oder stürzt.
- Idealerweise wählt man den Massepunkt dort, wo der reale Schwerpunkt wäre. Deshalb sind bei einem Klotz die Pfeile oft auf die Mitte gerichtet.
Aufpassen muss man, wenn effektiv Kräfte am gleichen Körper an verschiedenen Stellen angreifen, z.B wenn man einen Nagel einschlägt und dort eine Schnur anbindet. Denn so kann ein Drehmoment entstehen.
Oder wenn eben auf der schiefen Ebene nicht ein Klotz, sondern eine Kugel sitzt (rutscht die Kugel nur oder rollt sie? -> Ohne Reibung rutscht sie, mit rollt sie.)
Auf dem Bild ist die normalenkrsfr wie du sie definierst vom zentrum der Unterlage aus nach oben gerichtet
Ja. Wenn man nicht den Masse-Punkt nimmt, dann kann man das Zentrum (den Schwerpunkt) des Körpers nehmen.
Bei der Zeichnung von Lageplan der Kräfte geht es ums ungefähre Verstehen und Analysieren.
Beim Additionsplan kann man sichd dann ganz von der Zeichnung lösen. Nur die Richtung der Kraftvektoren muss erhalten bleiben, und die Längen (z.B. möglichen oder zu erwartenden resultierenden Kraft) ergeben sich dann aus der Geometrie.
Mit den andern Ansatz (auch in der Wiki-Zeichnung) ist es offenbar einfacher, die Ruhe des Körper darzustellen, weil je zwei Kräftepaare sind, wo sich zwei entgegengerichtete Kräfte gegenseitig aufheben und keine Vektoraddition im Dreieck gemacht werden muss.
Ok deine Erklärung ergibt für mich auch am meisten Sinn aber es muss doch einem unterschied geben ob die normalkraft nach unten zeigt odermach oben. Musst nicht eins von beiden dann falsch sein ?
Im Internet stand auch das die normalkraft senkrecht zur Unterlage wirkt aber als Angriffspunkt den massepunkt der Unterlage hat. Wie soll man das verstehen? Eine Zeichnung hierfür befindet sich auf Wikipedia.
Ja DAS ist definitiv sinnfrei (Kraft nach unten und Angriffspunkt an der Unterlage selbst). In welchem Wikipedia-Artikel hast du das gefunden? (Link bitte)
Der Unterschied ist eben die verschiedenen Lehrmeinungen:
- Meine versucht es mit Newton, das klappt bei allen Problemen, nicht nur bei der schiefen Ebene
- Die andere soll wohl so eine vereinfachte Schülerversion sein, die ohne Vektrorbetrachtungen auskommen kann und deshalb auch Newton ausblenden muss.
Weil ich meine die Kugel drückt ja auf den Untergrund drauf müsste dann nicht auch die normalkraft nach unten zeigen?
Die Interpretation der Normalkraft führt tatsächlich immer wieder zu Problemen. Wie gesagt gibt es zwei "Lehrmeinungen".
Ich halte mich an Newton, dann kann man logisch und konsequent argumentieren:
- Im Gleichgewicht hat jede Kraft hat eine Gegenkraft
- Für eine Zustandsänderung (also der Geschwindigkeit oder der Richtung) braucht es eine resultierende Kraft verschieden von null
In meinen Erklärungen tritt die Normalkraft von unten nicht einfach so auf, und schon gar nie alleine! Bei mir ist die Normalkraft die zwingend nötige Reaktionskraft nach Newton auf die immer senkrecht wirkende Gravitationskraft Fg. Bzw. noch genauer auf jene Komponente von Fg, die senkrecht zur Unterlage wirkt (und oft auch als Normalkraft bezeichnet wird).
Nur so kann man diese tatsächlich vorhandenen Kräfte vektoriell addieren.
(Wenn man hingegen eine nach unten wirkende "Normalkraft" mit der "Tangentialkraft" addiert, bekommt man eben wieder einzig die senkrechte Gravitationskraft, und so müsste der Körper nach Newton senkrecht abstürzen...)
Die Normalkraft kann höchstens gleich gross sein wie die Gravitationskraft, deshalb fängt der Körper auch nie spontan an zu schweben.
Aber vielleicht gibt es Leute, die mit der andern Lehrmeinung ebenso gut argumentieren können...
Erstmal vielen Dank für die Erklärung richtig gut!
Aber nochmal zu den Kräften. Wie soll man die richtigung der Kräfte verstehen? Ich meine die normalkraft drückt ja von unten auf den Körper. Aber müsste sie ihn dann nicht eigl weg vom Boden oder Ebene je nachdem drücken?
Ergänzend zu 1 noch die normalkraft wie du sie eingezeichnet hast also in umgekehrter Richtung und die hangabtriebskraft haben doch auch gar nicht den gleichen Angriffspunkt d.h. Man kann sie nicht addieren oder?
Zu 1:
Ja, die Kräfte Gravitation und Normalkraft sind vorhanden. Bei horizontaler Ebene ist es wohl klar, wenn nur die Gravitation wäre, würde der Stein ja ins Bodenlose stürzen. Wenn man den Boden nun schief stellt, verschwindet die Normalkraft sicher nicht schlagartig und schon gar nicht zeigt sie plötzlich in die andere Richtung. Das ist eben völliger Blödsinn in vielen Lehrbüchern.
Weil die Bewegung des Steins nach unten beschränkt ist, kann er sich nur entlang des schiefen Bodens bewegen. Somit ergibt sich eben aus Normalkraft und Gravitationskraft durch Vektoraddition die resultierende Kraft entlang der Ebene, welche am Schluss zum Abrutschen des Steins führen kann (bei fehlender Reibung oder bei genügender Steilheit).
Zum Angriffspunkt: Ja, da muss man aufpassen, bei nicht gleichem Angriffspunkt oder parallelen Wirkungslinien kann sich auch ein Drehmoment ergeben. Nur macht man hier meist eine stillschweigende Vereinfachung: Man betrachtet das Objekt (Stein) als Masse-Punkt. So haben dann alle Kräfte sicher den gleichen Angriffspunkt. Mögliche Rotationen müssen so sicher nicht beachtet werden.
Zu 2:
Zunächst als Wiederholung: Setze nicht Kraft mit Energie gleich.
Ja, die Reibung wird mit zunehmender Steilheit kleiner, dafür steigt der Aufwand, um die Höhe zu überwinden, weil die Hangabtriebskraft steigt. Die beiden Kräfte ersetzen sich also, sie heben sich nie auf.
Und man kann nicht ohne weitere Angaben sagen, ob es mehr Energie (Arbeit) braucht, den Stein 1m senkrecht hochzuheben, 1m auf der schiefen Ebene zu ziehen, oder 1m auf der horizontalen Boden zu ziehen.
Wenn die Reibungszahl kleiner als 1 ist (was meist so ist), dann ist alles einfacher als senkrechtes Anheben.
Wenn sie aber grösser als 1 ist (seltene Materialien), kann horizontales Ziehen sogar die grössere Kraft und über die gleiche (z.B. 1m) Länge auch mehr Energie erfordern.
Zu 3:
Die Reibungskraft hängt ab:
- von den reibenden Stoffen (von beiden Oberflächen), ja, natürlich, das sind die Reibungskoeffizienten
- von der Normalkraft ("Auflagekraft") Das kannst du mit Kratzen oder mit Schleifpapier selber erfahren.
Sie hängt nicht (oder im Idealfall und bei homogenen Körpern vernachlässigbar) ab: Von der Auflagefläche.
Denn wenn du eine bestimmte Normalkraft auf mehr Fläche verteilst (z.B. 4x soviel), ist zwar der Anteil jeder einzelnen Teilfläche an der Reibungskraft kleiner (1/4), aber eben die Anzahl "Bremsklötze" entsprechend (4x) grösser, das hebt sich in der Wirkung auf.
Zu 1: aber sind die beiden Kräfte dann wirklich vorhanden ? Weil die gravitationskraft wirkt ja immer. In der Flächen Ebene ist die normalkraft auch vorhanden, dh die beiden sind ja unabhängig voneinander (weil die normalkraft ja durch den Boden erzeugt wird). Wieso kann man das dann so einfach zerlegen?
Zu 2: ok ich muss die hangabtriebskraft kompensieren aber wenn die Reibung ja auch kleiner wird hebt sich das dann nicht wieder quasi auf? es müsste doch eigl mehr enegrie aufgebracht werden als in der Flachen Ebene wegen dem Höhenunterschied?
Zu 3: warum hängt die Reibungskraft von der normalkraft ab? Müsste sie nicht vom reibenden stoff und der Auflageflöche abhängen?
In der Skizze ist der Klotz eingezeichnet, der hochgeschoben wird. Auf den Klotz wirken drei Kräfte
1) Die Gewichtskraft FG = m * g nach unten
2) Die Normalkraft FN der Ebene AUF den Klotz nach links oben (Aufpassen: Nur in diesem Kindergartenbeispiel ist FN identisch mit der Normalkomponente der Gewichtskraft, die in vielen deutschen Physikbüchern leider als FN bezeichnet wird)
3) Die Reibkraft FR entlang der Ebene nach links unten (entgegen der Bewegungsrichtung)
Im Bild siehst du links den Klotz mit den drei Kräften.
Im Bild rechts sind die drei Kräfte vektoriell addiert, die rote Kraft Fres ist dann die resultierende Kraft auf den Klotz (vom Anfang der ersten bis zum Ende der letzten Kraft)
In diesem Trapez kann man nun mit geometrischen Überlegungen Fres berechnen, es ist
Fres = FR + FG * sin(alpha) = m * g * cos(alpha) * mü + m * g * sin(alpha)
Die erforderliche Energie ergibt sich nun aus der Länge der Rampe (Achtung: Das ist die Schräge, nicht die Höhe) zu
E = Länge * m * g * (mü * cos(alpha) + sin(alpha).
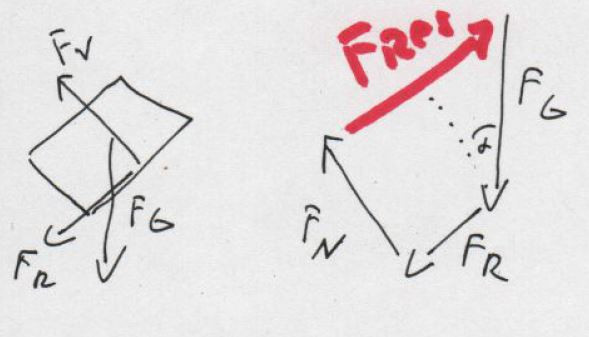
ACHTUNG: Der rote Pfeil geht natürlich von rechts oben nach links unten!
Bei einer flachen Ebene ist alpha = 0 , sin(0) = 0, cos(0) = 1 und damit
E = Länge * m * g * mü
Bei einer senkrechten Ebene ist alpha = 90, sin(90) = 1 , cos(90) = 0 und damit
E = Länge * m * g
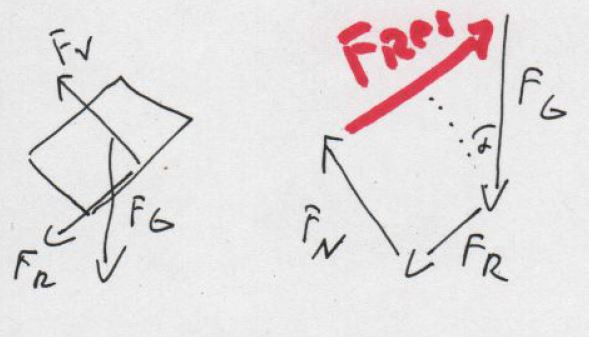
Aber warum kann man die Kräfte eingeschlafen addieren die haben ja nicht alle denselben Angriffspunkt
Das ist die Natur von vektoriellen Größen. Wenn du eine Kraft mit den Komponenten (2 , 3) hast und eine zweite mit den Komponenten (4 , 1), dann ergibt die Summe (2+4 , 3+1) = (6 , 4). Diesen Vektor erhältst du zeichnerisch , indem du (2 , 3) und (4, 1) einfach hintereinander setzt
Wichtiger als diese Sache, welche ja nur einfach die mathematische Vektoraddition und nichts besonderes ist, ist aber eine physikalische:
Wenn du Kräfte einzeichnest, dann darfst du in einem Bild auch nur EINEN Körper zeichnen, für diesen interessierst du dich in diesem Moment. Alle Kräfte, die nun eingezeichnet werden, betreffen dann nur DIESEN Körper und keine anderen, genauso, wie es in meinem linken Bild und in den Bildern von atoemlein eingezeichnet ist. Das bedeutet auch: In einem richtigen Kraftbild, in dem also nur 1 Körper eingezeichnet ist, kann man also niemals Actio und Reactio sehen, denn diese Kräfte beziehen sich auf zwei verschiedene Körper.
- Die Hangabtriebskraft Fh und die Normalkraft Fn sind wirkliche Kräfte,die sich aud der Gewichtskraft Fg=m*g ergeben.
Fg wird hier nur zerlegt in die Komponenten Fh und Fn
siehe Physik-Formelbuch
Arbeit W=F*S
Gleichgewichtsbedingungen an der schiefen Ebene:
Die Summe aller Kräfte in eine Richtung ist zu jeden zeitpunkt gleich NULL.
1) eine Zeichnung machen
2) die Kräfte an der Masse m antragen
ergibt F-Fh-Fr=0
Fh Hangabtriebskraft wirkt nach unten entgegen der Kraft F
Fr ist die Reibkraft.Diese wirkt immer entgegen der Bewegungsrichtung
F=Fh+Fr mit Fh=Fg*sin(a)=m*g*sin(a) und Fr=u*Fn=u*Fg*cos(a)=u*m*g*cos(a)
F=m*g*(sin(a)+u*cos(a)
ergibt W=F*s=m*g*(sin(a)+u*cos(a)*S
u ist der Reibwert zwischen der Masse m und der Unterfläche
Mit den Energieerhaltungssatz kannst du die Aufgabe auch rechnen.
1) Epot=m*g*h
2) Reibarbeit Wr=Fr*s=u*m*g*cos(a)
Gesamte Arbeit Wges=Wr+Epot
Ah das macht Sinn. Wenn ich aber schief ziehe brauche ich ja mehr Kraft um denselben Weg zurückzulegen und bekanntlicher weise ist ja die Energie die ich dafür aufwende gleich s*Fs also Kraft in Wegrichtung. Was passiert aber mit der Kraft die in vertikale Richtung zeigt? Verbrauche ich mit der auch Energie?