Radius mit Satz des Pythagoras rechnen?
Ich habe irgendwie das Gefühl, man kann bei a) das mit dem Satz des Pythagoras ausrechnen. Aber wie? Oder geht das ganz anders?
4 Antworten
Was dir für die Anwendung des Pythagoras fehlt ist das Stück vom Mittelpunkt bis nach oben zur Kreissehne. Das aber hat die Länge r - h. In den Pythagoras einsetzen und die quadratische Gleichung lösen.
Dieses "durchhangeln" von gegebenen Größen zum Ziel musst du üben üben üben.
Folgende Formel für Radiusberechnung.
r = ( (s/2)^2 + h^2 ) / (2 * h)
r = ((180/2)^2 + 57^2) / (2*57)
Wie kommst du auf diese Formeln? Siehe die Antwort von @Halbrecht und meine.
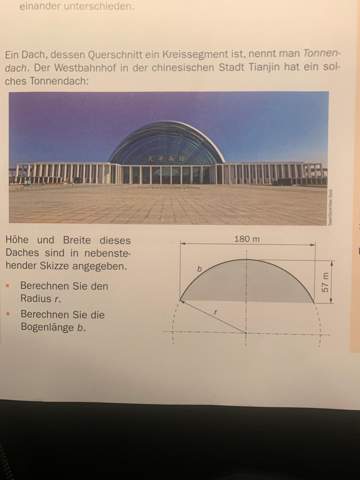
schau dieses Dreieck :
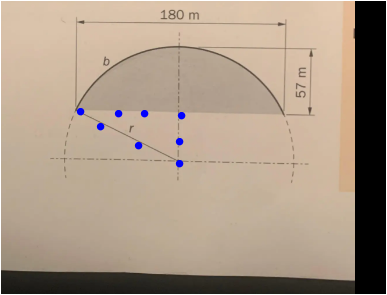
Nur eine Seite ist gegeben (90) . Sieht schlecht aus . Aber die senkrechte kann man als r-57 ausdrücken.
so und dadurch
r² = 90² + (r-57)²......................glücklicherweise fällt nach dem Ausmultiplizieren das r² weg.
.
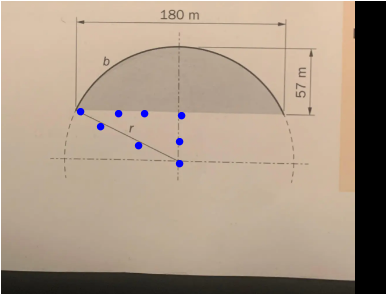
Könnte man prinzipiell schon, aber ich sehe keinen Weg wie du auf die Länge dieser kürzeren nach unten gerichteten Seite beim rechten Winkel kommst.
aja stimmt, ich bin einfach zu dumm, ich wusste es geht irgendwie, habe es aber einfach nicht gefunden