Querschnittsfläche eines Kanals?

Hey, ich hab die Aufgabe die Querschnittsfläche eines Kanals zu berechen und habe dafür eine Funktion 3. Grade gegeben. Eigentlich dachte ich man kann diese mit dem Integral berechnen doch bei mir kommt ein anderes Ergebnis als in der Lösung raus. Hat jemand vielleicht einen anderen Versuchsansatz?

Beste Grüße

Comments

[Elumania]

kann man mal die Aufgabe mit Grafiken falls es die gibt sehen?

[Jakii803]

Also Funktion ist f(x)=x^3+3x^2-2x-6

Answer 1

[Elumania]

Integral:

$F\left(x\right)\ =\ \frac{x^4}{4}+x^3-x^2-6x+C$

Einsetzen der Integrationsgrenzen. Obere Grenze W(2) minus untere Grenze -W(2)

$\left[\frac{4}{4}+2\sqrt{2}-2-6\cdot\sqrt{2}\right]-\left[\frac{4}{4}-2\sqrt{2}-2+6\cdot\sqrt{2}\right]=-6,65-4,66=-11,3$

Comments

[Jakii803]

Wäre dann an F(x)=1/4 x^4 +3x^3-2x^2-6x+c falsch ?

[Elumania]

@Jakii803

Hast du ein anderes Ergebnis als meins, dann ist deins falsch so leid es mir tut. 😅

Leite deine Funktion doch mal ab!

Da käme ich auf

f(x) = x³ + 9x² -4x -6

statt f(x)=x³+3x²-2x-6

[Jakii803]

@Elumania

Fehler gefunden, wahrscheinlich Tippfehler, vielen Dank für die Hilfe.

[Elumania]

@Jakii803

Alles klar, gerne!

Answer 2

[Halbrecht]

Ansatz korrekt . Vermutung : Rechenfehler oder falsch integriert :

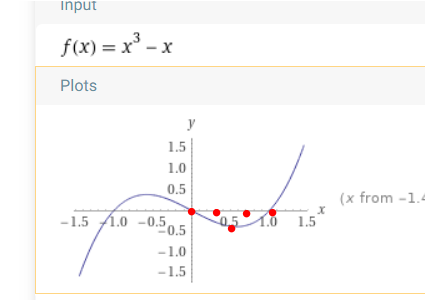
kanal von 0 bis 1

Fläche mit 1/4 * x^4 - 1/2 * x .............1 einsetzen minus 0 einsetzen ( ober minus untergrenze . Wegen der 0 ist die Fläche hier 1/4 - 1/2 = -1/4 . also 0.25 FE.

Comments

[Jakii803]

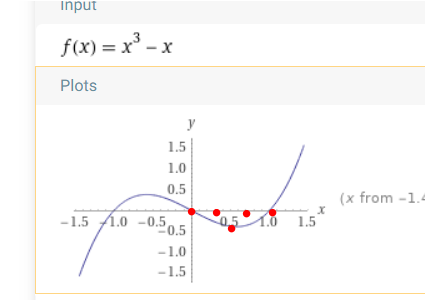
Ich hab bei meiner Fkt. noch eine oben liegende Parabel (bei ihnen im Bild, im I [-1;0]), aber wenn die Aufgabe mich nur nach dem Querschnittes des Kanals fragt, dann kann ich das dann weglassen oder?

[Halbrecht]

@Jakii803

ohne bild ich das nicht gut denken kann :)) bitte posten , ganze aufgabe . Vielleicht hat die Par doch einen Anteil am richtigen Ergebnis.

[Jakii803]

@Halbrecht

Fehler bereits gefunden, dennoch vielen Dank.

[Halbrecht]

@Jakii803

und wo war der Fehler ?

Answer 3

[Elumania]

f(x)=x^3+3x^2-2x-6

Was sind die Integrationsgrenzen?

-3 und -Wurzel(2) ?

Comments

[Jakii803]

Ich glaube weil nur der Kanal gesucht ist -Wurzel 2 und + Wurzel 2

[Elumania]

@Jakii803

Da kommt -11,3 raus bei dem Integral. Ist das richtig mit der Lösung?

[Jakii803]

@Elumania

Ja, das ist die Lösung, aber wie? Ich komme nur auf -6