Quadratische Pyramide?
Hallo,
eine Frage. Die Aufgabe sagt ja, dass der parallelschnitt des dreiecks gleichseitig ist. Also alle drei seiten sind gleich lang = 7.5cm. Gilt dann nicht für h aber für h_s und a und wieder h_s = 7.5cm. Habe als ich dann h_s berechnet habe, kam 8.39cm raus. Warum? Sollte es nicht 7.5cm sein??


Aufgabe a nicht b.
2 Antworten
Du hast die falsche Seite berechnet. Die Höhe ist die Seite, die in der Mitte Pyramide steht, diese ist nicht 7,5 cm groß. Daher klappt Wurzel aus (7,5² + 3,5²) auch nicht, du musst sie umstellen (a² + b² = c² -> c² - a² = b²).
Höhe sollte also etwa 6,5 sein.
Wenn du dir die Vorderseite des Dreiecks anschaust, entspricht sie meinem Screenshot. Die Höhe kann nicht 7,5 cm betragen, denn sonst wäre die Hypotenuse gleich 8,38.
P.S. die gesuchte Höhe ist die Seite, die das Dreieck in der Mitte halbiert.
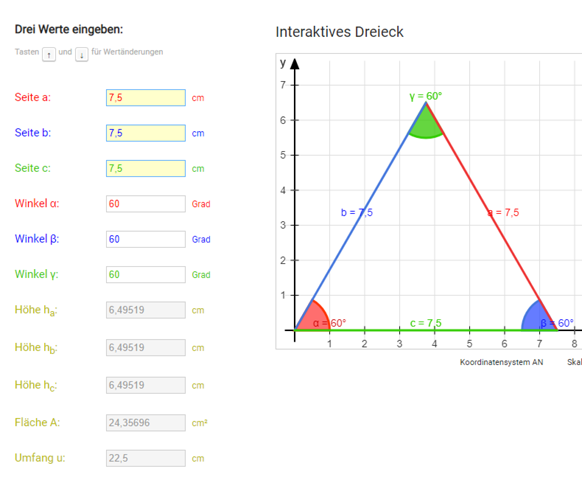
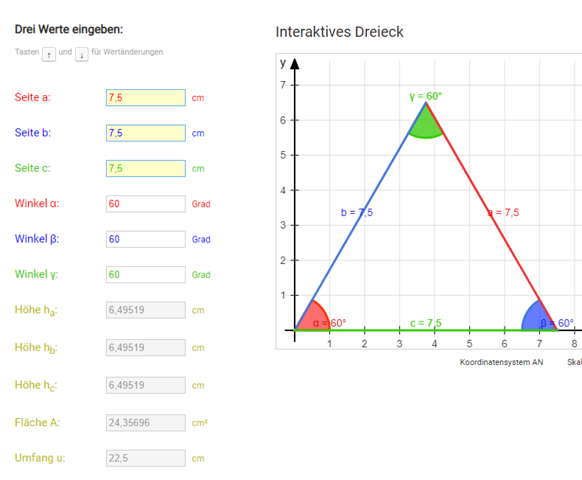
Die 8, 39 sind falsch.
Du hast die Formel falsch angewendet.
a² + b² = c²
3,75² + ? = 7,5²
Die 7,5 cm sind die längste Seite im rechtwinkligen Dreieck.
Aber die Formel lautet:
h_s^2 = h^2 + (a/2)^2 . Steht auch so im Buch.. Aber ja ich denke dann falsch angewendet. Ich dachte, man müsste das ganze rote dreieck nutzen, aber dann wäre phytagoras auch nicht mehr nutzbar.. okay. Soweit danke.