Möndchen des Hippokrates (zeige,dass die gelbe Fläche den gleichen Inhalt wie die grüne hat)?
Hey,ich wollte fragen,wie man das berechnen kann.Leider verstehe ich das Ganze nicht so.Danke im Voraus!:)
Zeige,dass die gelbe Fläche den gleichen Inhalt wie die grüne hat.

2 Antworten
Man sieht ja hier vielleicht, dass die Monde Halbkreise mit Radius r sind, denen genau die Fläche fehlt wurde, die auch dem Quadrat fehlt, damit es ein Kreis wäre.
Sagen wir also, beide hätten diese Fläche stattdessen, dann ändert sich ja am Verhältnis nichts, beide haben noch die gleiche, wenn auch nun etwas größere, Fläche.
Beachte, dass du die 4 Halbkreise zu 2 ganzen Kreisen mit Radius r zusammensetzen kannst.
Die Strecke von der Mitte des Quadrates zu einem seiner Ecken ist ja r*sqrt(2). (Denn a²+b²=c² in einem rechtwinkligen, gleichschenkligen Dreieck -> a=sqrt(2)c).
Nun ist die Kreisfläche ja pi*r².
Dann haben wir 2 kleine Kreise mit Radius r und Fläche pi*r², insgesamt 2(pi*r²)
Und einen großen Kreis mit Radius r*sqrt(2) und Fläche pi*(sqrt(2)*r)²=2(pi*r²)
Somit sind beide Flächen gleich.
Ich weiß nicht genau, wo das r jetzt steht (an der senkrechten oder diagonalen Linie), deswegen nehme ich für meine Rechnung an, es steht an der senkrechten Linie. Funktioniert aber auch anders, nur dann mit anderen Zahlen.
Die kleinen Kreise hätten dann als Radius r/sqrt(2)=r*sqrt(2)/2 und der große einfach r.
Man sieht ja hier vielleicht, dass die Monde Halbkreise mit Radius r sind, denen genau die Fläche fehlt wurde, die auch dem Quadrat fehlt, damit es ein Kreis wäre.
Mir kommt es eher so vor, als ob die
gelben Monde Halbkreise mit Radius a/2
sind, wenn a die Kantenlänge des Quadrats ist.
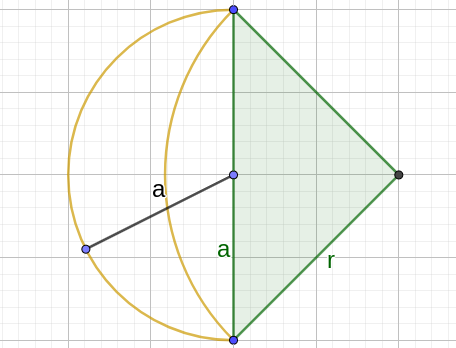
Es hilft, die Form zu zerlegen. Die Form ist symmetrisch, besteht also aus 4 identischen Teilen. Es reicht also, zu beweisen, dass in folgender Form das grüne Dreieck gleich groß wie der gelbe Halbmond ist:

Hier habe ich außerdem den Radius a der äußeren Kreislinie eingezeichnet. Laut Pythagoras ist a² + a² = r² bzw. r² = 2 · a²
Nun können wir die Fläche des grünen Dreiecks berechnen:
Der gelbe Halbmond ist etwas schwieriger, aber nicht unmöglich: Zuerst berechnen wir den Flächeninhalt des gelben Halbkreises mit Radius a, dann ziehen wir das ab, was wir zuviel berechnet haben: Die Sichel zwischen dem gelben Mond und dem grünen Dreieck.
Die Sichel wiederum lässt sich berechnen, indem man 1/4 des inneren Kreises berechnet, und die grüne Fläche abzieht:
Damit hat der gelbe Halbmond folgende Formel:
Um r² loszuwerden, kann man die oben genannte Formel r² = 2 · a² verwenden:
Und hier hast du die Lösung: Beide Flächen haben den Flächeninhalt a².
Stimmt leider nicht. Der große, weiße Kreis hat den Radius r. Die äußeren Kreislinien der gelben Monde haben einen anderen Radius. Es sieht so aus, als wäre dieser Radius die Hälfte der Seitenlänge des grünen Quadrats. Demnach haben die gelben Halbmonde den Radius r / sqrt(2).