Wie rechnet man den Inhalt der Fläche unter dem Graphen aus?
Hallo ich brauche Hilfe bei der Aufgabe:
- Berechnen Sie den Inhalt der Fläche unter dem Graphen von f über dem Intervall I.
fertigen Sie zuächst eine Skizze an.
f(x) = x²-6x+5 I= [1;5]
ich versuche es die ganze Zeit und verstehe einfach nicht wie das gehen soll.+
8 Antworten
Stammfunktion F(x) bilden, das heißt: du suchst eine Funktion, die, wenn sie abgeleitet wird, f(x) ergibt. Diese solltest du (leicht) finden
Anschließend F(5)-F(1) rechnen
Dankeschön habe das soweit verstanden :)
Kannst du mir sagen wie man aus dem ganzen eine Skizze bildet?
mfg
Tobi
Hier musst du integrieren und dann die Grenzen einsetzen
A=\int_(1)^(5) (x^2-6x+5)dx =[1/3x^3-3x^2+5x]_(1)^(5)=(1/3*5^3-3*5^2+5*5)-(1/3*1^3-3*1^2+5*1)
Tut mir leid, ich struggle etwas mit dem Formeleditor, ich schicke dir gleich meinen Rechenweg
Erst mal ist nicht die Fläche unter dem Graphen
gemeint - die ist unendlich groß - sondern
die Fläche zwischen dem Graphen und der x-Achse.
Du berechnest das Integral bzw. die Stammfunktion F(x)
und rechnest dann F(5) - F(1) aus. Das ist negativ; da die
Fläche gesucht wird, nimmst du den Betrag davon.
Erst mal ist nicht die Fläche unter dem Graphen
gemeint - die ist unendlich groß - sondern
die Fläche zwischen dem Graphen und der x-Achse.
Oha, stimmt. Ich nehme die X-Achse immer implizit an.
Gruß
Stammfunktion bilden:
F(x) = 1/3x^3 -3x^2 + 5x + x
F(5) - F(1) =
-25/3 -7/3
= -10,6666 FE
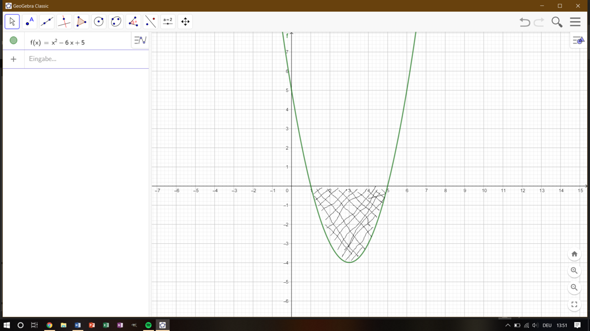
So in etwa skizzieren :)
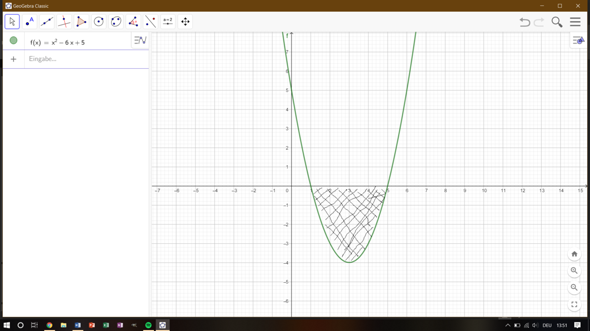
Danke :)