Maximalen Definitionsbereich einer Funktion bestimmen?
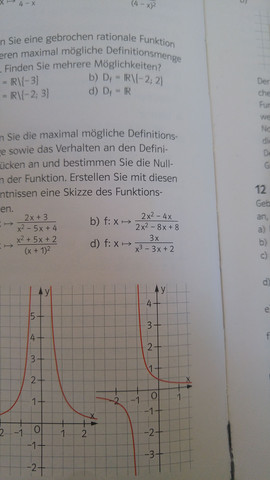
Hallo! Ich hänge grad an einer Aufgabe und würde mich über Hilfe freuen! Man soll den maximalen Definitionsbereich bestimmen, dazu muss man den Nenner ja 0 setzen, um eben die Definitionslücken rauszufinden. Der Nenner ist aber ein Polynom 3. Grades und ich weiß nicht wie ich die Nullstellen da finden kann, da die Polynomdivision nicht aufgeht. Auf dem Bild Nummer d)
Ich bin dankbar für alle Antworten!!
3 Antworten
Kannst Du, wie in diesem Fall, kein x ausklammern, weil Du einen Summanden ohne x hast, dann hilft erst einmal nur raten.
x=1 wäre eine Nullstelle. Nun musst Du die Polynomdivision anwenden, indem Du diesen Polynom durch "x MINUS Nullstelle" teilst, also:
(x³-3x+2) : (x-1) = ... und das muss aufgehen, sonst wäre die erratene Nullstelle keine Nullstelle (z. B. Rechenfehler)
Die Polynomdivision geht für x=1 nicht auf?
Bei mir schon
Kommt x²+x-2 raus
Sieht für mich nach einer Parzialbruchzerlegung aus