Mathe Textaufgabe?
Vielleicht kann mir jemand erklären wie ich zur Lösung komme?
(Gleichung????)
Ein Zug fährt einem anderen von einer 80 km entfernten Station
entgegen. Sie treffen sich nach 32 Minuten, wenn sie gleichzeitig
losfahren. Fährt der eine 15 Minuten früher los als der andere, treffen
sie sich nach 40 Minuten. Wie schnell fahren die beiden Züge in km/h?
Vielleicht hilft mir jemand weiter mit der Aufstellung eines linearen Gleichungssystems, damit ich die Geschwindkeit von Zug 1 und 2 errechnen kann.
2 Antworten
Mein Ansatz wäre folgender.
Egal, wann die Züge losfahren und wie schnell sie fahren, wenn wir die Bewegungen der Züge von dem Moment betrachten, an dem sie losfahren, bis sie sich treffen, dann haben beide Züge zusammen immer die Gesamtstrecke von 80 km zurückgelegt. Das leuchtet ein, oder?
Das kann man dann ganz einfach mit folgender Bewungsgleichung ausdrücken:
v_Z1 und v_Z2 sind die jeweiligen Geschwindigkeiten; t₁ und t₂ die jeweiligen Fahrtdauern; s die Strecke.
Im ersten Szenario sind t₁ und t₂ identisch, im zweiten Fall ist t₁ 15 Minuten länger als t₂ (oder kürzer, je nachdem, welchen Zug du als Zug 1 bezeichnest).
Die Zeiten sind gegeben, die Gesamtstrecke auch.
Also kannst du diese allgemeine Gleichung auf die beiden Szenarien anwenden, erhälst zwei Gleichungen, in denen nur noch die jeweiligen Geschwindigkeiten zu ermitteln sind.
Dieses lineare Gleichungssystem löst du dann so, wie sonst auch.
Ich könnte dir natürlich die komplette Rechnung aufschreiben, aber du lernst mehr, wenn du hier selber weitermachst.
Probier mal, wie weit du kommst, und wenn du stecken bleibst, kannst du dich gerne noch mal melden! 😀
evtldocha hat dir doch (bedauerlicherweise wie ich finde) schon alles heruntergebetet.
Dass du uns beide trotzdem quasi zeitgleich fragst, dir die Gleichungen hinzuschreiben, lässt mich vermuten, dass du deine Hausaufgabe einfach nur abschreiben willst, und das werde ich nicht unterstützen.
Ich helfe Leuten gerne, Dinge besser zu verstehen, aber ich bin nicht der Hausaufgabendepp für andere.
Ich will dir mal glauben. Leider benutzen etliche Schüler diese Plattform, um ihre Hausaufgaben zu delegieren und die Tatsache, dass du dich offensichtlich extra für diese Frage angemeldet hast, verstärkt diesen Eindruck.
Ich verstehe auch nicht so ganz, welchen Vorteil es haben soll, x und y für die Geschwindigkeiten zu benutzen. v ist die übliche Abkürzung für Geschwindigkeiten und die tiefgestellte 1 bzw. 2 lässt sich besser den entsprechenden Zeiten zuordnen.
Aber natürlich kannst du das auch austauschen, wenn's unbedingt sein muss.
Wie gesagt, ich würde den Ansatz wählen, dass ich mir für beide Szenarien die jeweilige Strecke anschaue, der von Zug X und Zug Y gefahren wird, weil sich diese immer zu 80 km aufaddieren. (Denn das ist ja die Gesamtstrecke, die von beiden Zügen zusammengenommen gefahren wird, nur dass die sich von unterschiedlichen Seiten nähern.)
Strecken berechnen sich ja nach der Formel s=v⋅t (das ist das v wieder!), was du vielleicht noch aus dem Physik-Unterricht kennst.
Jeder Zug hat seine eigenen Geschwindigkeit und seine eigene Zeitdauer, die wie gesagt im ersten Szenario gleich, im zweiten aber Unterschiedlich ist. Beide Strecken, die von Zug X und Zug Y addieren sich immer zu 80 km.
Das ist die etwas ausführlichere Erklärung zu der Gleichung, die ich in meiner ursprünglichen Antwort hingeschrieben habe.
Wenn wir die Werte des ersten Szenarios einsetzen erhalten wir daher:
(I) x ⋅ 32 min + y ⋅ 32 min = 80 km
Für das zweite Szenario wird es etwas komplizierter, weil man hier das spätere Losfahren des zweiten Zuges berücksichtigen muss. Wenn Zug Y der Zug ist, der später losfährt, dann erhalten wir diese Gleichung, wobei X jetzt eine Fahrzeit von 40 Minuten hat, Y aber eine um 15 Minuten verkürzte, d.h. 25 Minuten:
(II) x ⋅ 40 min + y ⋅ 25 min = 80 km
Die Gleichungen I und II sind das gewünschte lineare Gleichungssystem.
Magst du versuchen, das zu lösen oder soll ich es auch noch durchrechnen?
Nein, die Aufgabe ist alles andere als stupide. Ich hatte in der Schule Mathe- und Physik-LK, insofern fällt mir das leicht, aber ich erwarte nicht, dass das für andere auch so ist. (Genauso wie ich vieles nicht kann, was für andere ein Kinderspiel ist.)
Viele Schüler sind von dieser Art Aufgabe wenig begeistert, weil sie offensichtlich halt doch Schwierigkeiten bereitet.
Das größte Problem ist allerdings, die Gleichungen aufzustellen, was ich ja schon gemacht habe. Der Rest ist die Anwendung von Standardmethoden, wie man lineare Gleichungssysteme löst.
Ich kann dir das Beispiel mal schnell durchrechnen, aber wenn du das auffrischen willst, empfehle ich dir, mal auf YouTube nach entsprechenden Videos zu schauen. Das gibt es mehrere gute Leute, die das erklären.
Ich rechne hier auch mit Einheiten, weil ich das als sauberer empfinde und das Mitnehmen von Einheiten auch als Fehlerkontrolle dienen kann. Viele lassen bei reinen Matheaufgaben Einheiten aber weg und schreiben sie ggf. ganz am Ende wieder dazu (wie es evtldocha in seiner Rechnung gemacht hat).
Ich fange mit Gleichung I an, weil die einfacher ist und löse sie nach einer Variable auf:
x ⋅ 32 min + y ⋅ 32 min = 80 km | Ausklammern von 32 min
32 min ⋅ (x + y) = 80 km | auf beiden Seiten durch 32 min teilen
x + y = 80 km / 32 min = 2,5 km/min
Jetzt kann man sich entscheiden, ob man nach x oder y auflöst. Hier ist beides gleich schwer oder einfach. Ich löse mal nach y auf:
y = 2,5 km/min - x
Jetzt haben wir y als eine Funktion von x dargestellt und können das in Gleichung II einsetzen, sodass nur x als einzige Unbekannte vorkommt, nach der aufzulösen ist:
x ⋅ 40 min + (2,5 km/min - x) ⋅ 25 min = 80 km | Klammer ausmultiplizieren
x ⋅ 40 min + 62,5 km - x ⋅ 25 min = 80 km | alle x'e zusammenfassen
x ⋅ 15 min + 62,5 km = 80 km | den km-Wert auf die rechte Seite bringen und zusammenfassen
x ⋅ 15 min = 17,5 km | durch 15 min teilen
x = 17,5/15 km/min
Ich würde die Einheiten normalerweise erst am Ende der Rechnung umrechnen (es ist ja die Geschwindigkeit in km/h gefragt), aber weil wir hier einen Bruch dastehen haben, der in km/h eine glatte Zahl ergibt, mache ich das hier ausnahmsweise. Um die Einheit umzurechnen, multiplizieren wir formal mit dem Faktor 60 min/h:
x = 17,5/15 km/min ⋅ 60 min/h = 70 km/h
Mit diesem Ergebnis können wir jetzt mit der Gleichung von weiter oben y ermitteln, aber bevor wir das machen, bietet es sich an, dort die Einheit km/min ebenfalls in km/h umzurechnen:
y = 2,5 km/min - x
y = 2,5 km/min ⋅ 60 min/h - x
y = 150 km/h - x
Jetzt setzen wir den ermittelten Wert für x ein und erhalten y:
y = 150 km/h - 70 km/h = 80 km/h
Und das war's!
Zug X fährt mit einer (Durchschnitts-)Geschwindigkeit von 70 km/h, Y mit 80 km/h.
Ich hatte auch vergessen darauf hinzuweisen, dass die Art und Weise, wie ich das lineare Gleichungssystem gelöst habe, nur eine Möglichkeit von mehrere ist.
Man hätte z.B. beide von einander abziehen können, dann hätte man folgendes dastehen gehabt:
x ⋅ (-8 min) + y ⋅ 7 min = 0
Das kann man umformen zu:
7y = 8x, bzw. y = 8/7 x oder auch x = 7/8 y
Dann hätte man die Gleichung I wie zuvor gezeigt zu
x + y = 2,5 km/min
umformen und dann entweder x oder y ersetzen können, z.B. so:
7/8 y + y = 2,5 km/min
15/8 y = 5/2 km/min
y = 4/3 km/min = 80 km/h
Das wäre vllt geschickter gewesen.
Letztenendes kommt immer dasselbe raus, solange man richtig rechnet.
ja so ist es, ich habe jetzt so gerechnet : (Deshalb auch meine Anfangsfrage nach der Aufstellung der Gleichungen I und II)
Gleichsetzungsverfahren I) 32/60*x+32/60*y=80 |*60
II) 40/60*x+25/60*y=80 |*60
I') 32x+32y=4800 |:8
II') 40x+25y=4800 |:10
I') 4x+4y=600 |-4y
II') 4x+2,5y=480 |-25y
I') 4x=600-4y
II') 4x=480-2,5y
x Gleichsetzen I'= II' 600-4y = 480-2,5y |+2,5y ; -600
-1,5y=-120 |:-1,5
y=80
y=80 einsetzen in I') 32x+32y=4800
32x+32*80=4800
32x+2560=4800 |-2560
32x=2240 |:32
x=70
Lösung L(70|80)
Probe mit II') II') 40*x+25y=4800
40*70+25*80=4800
2800+2000=4800
4800=4800
Ja, so kann man es auch rechnen! Und ich sehe da keinen Fehler (außer einem vertippten -25y, das -2,5y sein sollte und auch so gerechnet wurde).
Bravo! 😀
Ich würde noch anmerken, dass die Rechnungen hier sehr verschieden ausfallen können, je nachdem wie man die Sache angeht.
Ich habe z.B. bis ziemlich am Ende mit km/min gerechnet (und in meiner privaten Rechnung auch bis ganz zum Schluss), und die Konversion in km/h erst spät gemacht. Du hast sie ganz zu Anfang gemacht und dann, um die Nenner loszuwerden, die Zahlen aufgebläht. Das ist nicht schlimm und absolut nicht verkehrt, macht halt nur die Zahlen groß. In meinem Fall bekomme ich früher oder später unschöne Brüche. Was da besser ist, kann man sich drüber streiten.
Man kann die Sache auch ganz unterschiedlich angehen.
Mein Ansatz hier war, wie gesagt, dass beide Züge immer genau die 80 km zurücklegen und ich habe die Gleichungen dementsprechend aufgestellt.
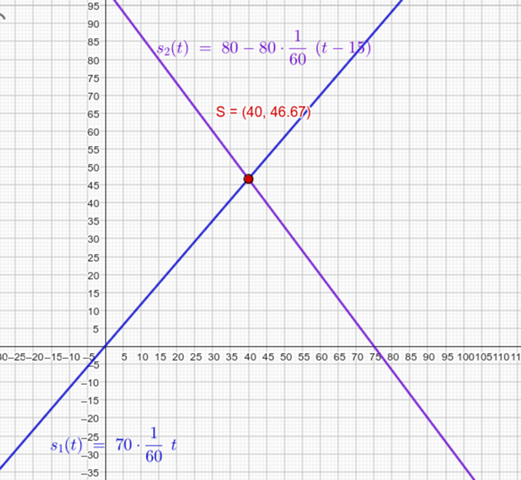
evtldocha, der ein sehr kompetenter Zeitgenosse ist, hat einen anderen Ansatz genommen. Dort hat er den Abstand des jeweiligen Zuges zum Ausgangspunkt von Zug 1 genommen und zwar für beide Züge. Dieser Abstand wächst für Zug 1 und verringert sich für Zug 2 (was man auch in der Graphik sieht). Sie treffen sich dort, wo der Abstand gleich ist.
Ein dritter Ansatz, mit dem ich gerne rechne, ist, eines der bewegten Objekte als Bezugsystem zu nehmen, das man als ruhend betrachtet.
Hier bringt das keinen direkten Vorteil und würde jemanden, der das noch nicht so oft gemacht hat, nur zusätzlich verwirren, deshalb habe ich das nicht erwähnt.
Alle diese Ansätze sind OK, letztenendes Geschmackssache.
Mit der Strecke in Kilometern und der Zeit in Stunden ergibt sich für (diese Wahl für t mache ich, damit das Ergebnis auch in km/h herauskommt. Man könnte t auch in Minuten rechnen, müsste dann aber die Geschwindigkeiten km/min noch in km/h umrechnen)
Zug 1:
Zug 2:
Informationen (Achtung: Ich lasse hier Zug 2 später abfahren. Das hat einen Einfluss darauf, welche Geschwindigkeit sich für den jeweiligen Zug ergeben wird)
Damit bekommst Du 2 Gleichungen für die gesuchten Geschwindigkeiten und dieses Gleichungssystem musst Du lösen.
Zur Kontrolle:
(siehe Anmerkung zur Annahme, welcher Zug später losfährt)
Skizze zur ersten Bedingung (Zeit in der Skizze ist in Minuten)

Skizze zur zweiten Bedingung


ich blick's leider nicht. Kannst du mir die 2 Gleichungen mit "x" für Geschw. Zug1
und y für Geschw. Zug 2 aufschreiben damit ich's nachvollziehen kann.
Welchen mathematischen Unterschied soll die Benennung von v1 = x und v2 = y. Verstehst Du damit irgendetwas besser, nur weil die Unbekannten anders bezeichnet sind? Ich glaube das nicht, aber wenn Du das unbedingt brauchst, ersetz' es selber. Mir ist das zu echt albern ...
tut mir leid dass ich*s nicht blicke. Trotzdem vielen Dank für die Mühe!
Das hat nichts mit "nicht blicken" zu tun, sondern ist pure Sturheit im Insistieren auf bestimmte Buchstaben. Und wenn Du was nicht blickst, kannst Du gerne fragen, was das genau ist. Aber bitte erzähl mir nicht, dass Dein "Nichtblicken" irgendwas mit der Bezeichnung / dem Buchstaben von gesuchten Werten zu tun hat.
Ich wollte dich auf keinen Fall so in Rage bringen. Ich beschäftige mich mit solchen Textaufgaben um mein Gedächtnis zu trainieren. Bin Jahrgang 1954 und hab deshalb nicht mehr ganz so den Durchblick. Ist auch alles schon ne Weile her. Also nicht's für ungut und nochmals Entschuldigung und Danke für die Mühe.
Ich bin nicht in Rage - nur entsetzt, was einen Menschen so blockieren kann, dass ihm Buchstaben so wichtig sind, dass er daran ein Verständnis eines Sachverhalts knüpft.
ich blick's leider nicht. Kannst du mir die 2 Gleichungen mit "x" für Geschw. Zug1
und y für Geschw. Zug 2 aufschreiben damit ich's nachvollziehen kann.