Mathe? Höhe des Flugzeugs berechnen?
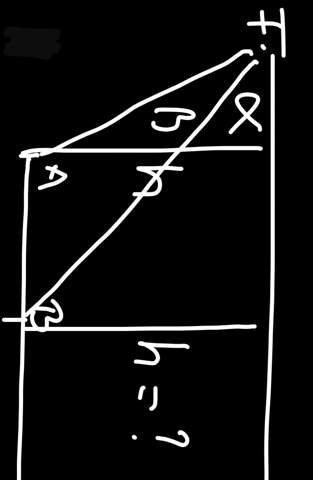
Hi ich komme nich mehr weiter. Ich hoffe ihr könnt mir helfen. Eine Skizze habe ich mal vorgezeichnet.
Von einem Flugzeug werden 2 vor ihm liegende, mit ihm in einer Vertikalebene befindliche Orte gleicher Seehöhe unter dem Tiefenwinkel alpha= 55,4° und betha= 68,8° angepeilt. Die Entfernung der Orte auf einer Karte vom Maßstab: 1:10 000 beträgt 4,5 cm.
Berechnen Sie die Höhe, in der sich das Flugzeug befindet.
Ich hoffe wirklich, das ihr mir hilft. Die Lösung sollte 1490,17 m sein.
4 Antworten
A, B und F bilden ein Dreieck, von dem Du 2 Winkel kennst, nämlich alpha im Punkt B und (180° - beta) im Punkt A - ich persönlich hätte die Punkte ja anders herum benannt ;-).
Außerdem kennst Du die Strecke [AB]. Mit diesen drei Angaben ist das Dreieck und damit die Lage von F eindeutig bestimmt.
Ich weiß jetzt gerade nicht, ob es eine einfache Formel gibt, um aus diesen Angaben die Höhe zu berechnen...
----------------------------------------------------
Ich persönlich würde die beiden "Sichtstrahlen" als lineare Funktionen betrachten und F daraus berechnen:
Du kennst von beiden jeweils einen Punkt bzw. Du kannst sie unter Berücksichtigung ihres Abstandes im Koordinatensystem festlegen, z. B. als (0|0) und (0|4,5), und Du kennst ihre jeweiligen Steigungswinkel alpha und beta, damit kann man die Funktionsgleichungen aufstellen.
Wenn man dann die beiden Gleichungen gleichsetzt und das Ganze nach x auflöst, erhält man die x-Koordinate von F, und durch Einsetzen in eine der Gleichungen dann die y-Koordinate - die ist dann (maßstäblich umgerechnet) die Höhe des Flugzeugs.
In welchem Dreieck soll denn BF die Hypotenuse sein?
ABF ist kein rechtwinkliges Dreieck ...
Nein aber die Höhe auf der Grundlinie AB durch F ergibt den Hilfspunkt "H" und das Dreieck AHF ist ein rechtwinkliges Dreieck.
Das Dreieck ABF hat die Höhe nun einmal außerhalb, wenn man AB als Grundseite betrachtet.
Ja, so weit war ich auch schon - aber von AHF kennst Du gar nichts, keine einzige Seite, wie willst Du da Pythagoras ansetzen?
Ich gebe dir recht, ich war im Kopf einen Schritt weiter als die Aufgabe. Es wird am Ende der Cosinussatz. Ich habe eine extra Antwort geschrieben, da ich hier wohl kein Bild einfügen kann.
Stimmt, auf Sinus- oder Cosinussatz als Lösungsansatz hätte ich auch kommen können, aber die habe ich irgendwie nie auf dem Schirm und kenne sie auch nicht auswendig - ich weiß gar nicht, ob ich die in der Schule gelernt habe...
Die Skizze ist falsch. Es sind zwei Punkte "A" und "B" die auf der selben Höhe liegen. bei dir ist "A" höher als "B"
In der Horizontalen ist die Strecke gegeben ( aus dem Maßstab umrechnen in eine Echte Länge)
Die Beiden Winkel bezogen auf die Horizontale definieren somit ein eindeutig berechenbares Dreieck.
Die Skizze ist nicht falsch, sondern nur um 90° verdreht - oder schreibst Du Buchstaben immer "auf dem Bauch liegend"?
gehe auf "mathelounge"im INternet registriere dich dirt, ist kostenlos. Dir wird inert 50 min in der Regel eine Antwort gegeben und du erhälst nachricht in deinem mail postfach dass du die Antwort erhalten hast.
Das ist echt super !
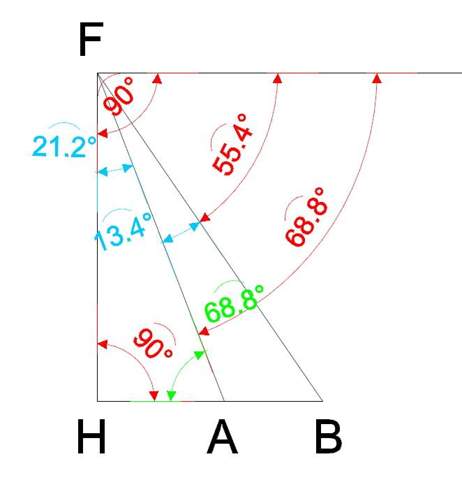
Also hier nochmal...
Gegeben sind (in rot) die Strecke AB sowie die Winke 68,8° und 55,4°
Ebenfalls die Winkel gegenüber der Horizontalen und der Vertikalen 90°
Daraus resultieren (in blau) die Winkel in AFB mit 13,4° und der Winkel HFA mit 21,2°.
Aus der Winkelsumme ergibt sich im Dreieck AHF der Winkel in A (grün). Nennen wir ihn "Alpha 1"
Dieser Winkel wiederum liegt auf der Geraden HB was aus der Reduktion von 180° zum Winkel "Alpha 2" (111,2°) führt.
Nun über die Winkelsumme im Dreieck ABF (180°-13,2°-111,2°) ergibt sich der Winkel in B --> 55,6°
Nun sind im Dreieck ABF 3 Winkel und eine Strecke gegeben.
Über den Cosinussatz lässt sich nun die Strecke BF berechnen. die dann im rechtwinkligen Dreieck BFH als Hypotenuse gilt.
Dann errechnet sich über den Cosinus die Seite HF was die Flughöhe ist.
Alternativ errechnet man auch die Strecke AF und kontrolliert die Flughöhe.
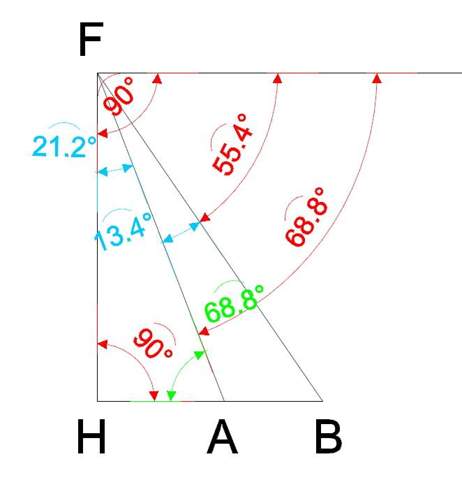
Na, die Winkel kann man aber auch schneller bestimmen:
- Bei B tritt Beta = 54,4° als Wechselwinkel wieder auf.
- Dein Alpha 1 ist Wechselwinkel zu Alpha, also auch 68,8°, bei A haben wir also als Nebenwinkel 180° - 68,8° = 111,2°.
Und bei F ergibt sich dann aus der Winkelsumme des Dreiecks 180° - 68,8° - 111,2° = 13,4° (den hast Du übrigens im Bild richtig eingetragen, Dich in Deiner Rechnung dann aber vertippt und 13,2 geschrieben, was dann zum falschen 54,6 bei B führt).
Allerdings erkenne ich noch nicht, wie Du dann mit dem Cosinussatz weiterkommen willst. Der benötigt zwei Seiten und den eingeschlossenen Winkel, um die dritte Seite zu berechnen, Du kennst aber nur eine. Ich denke - nachdem ich mir die Sätze jetzt noch mal angeschaut habe ;-) -, hier wäre der Sinussatz hilfreicher, da der aus zwei Winkeln und einer Seite eine zweite Seite berechnet. (Und dann können wir uns sogar die Berechnung des Winkels bei F sparen...)
Korrektur:
Natürlich können wir uns die Berechnung des Winkels bis F für den Sinussatz nicht sparen - das ist ja gerade der Winkel, der der einzigen bekannten Seite gegenüber liegt...
Die Formel liefert uns Pythagoras.
Mit den gegeben Werten berechne ich die Strecke B,F die im rechtwinkligen Dreieck die Hypotenuse bildet. Danach über die Sinusfunktion (Winke Alpha und Strecke B,F) ergibt sich "h".