Mathe Aufgabe rekursive Zahlenkette?
Guten Mittag,
kann mir wer bei folgender Aufgabe helfen? Ich verstehe weder, wie man auf die Zahlenreihe kommt, noch, was der Ausdruck a = max... bedeutet :)
Danke


Hier das Bild.
6 Antworten
max: Du musst alle a-Paare bilden mit n (ist ja vorgeben durch den Folgenindex) und d. Dieser "Index" ist lediglich dadurch definiert, dass d kleiner als n (aber größer als 0) ist.
Also bei n=4 haben wir folgende Menge möglicher d: [1,2,3]. Daraus ergeben sich folgende mögliche Paare a_d und a_(n-d): (a1, a3), (a2,a2),(a3,a1). Diese wollen paarweise multipliziert sein, also 0*3, 2*2 und 3*0, das Maximum daraus ist 2*2.
a_4 ist damit 4 = 2*2
Und dann geht es weiter mit a_5: Die d sind von 1 bis 4, also (a1,a4),(a2,a3) und die übrigen sind spiegelbildlich, damit 0*4, 2*3 = 6, a_5 = 6 = 2*3
a_6 = 3*3
a_7 = 2*2*3 (4*3)
a_8 = 2*3*3 (2*9)
a_9 = 3*3*3 (3*9)
a_10 = 18 * 2 = 12 * 3 = 9 * 4 = 3 * 3 * 2 * 2
Kannst Du damit die Folge explizit (also nicht-rekursiv) beschreiben?
Es ist zwingend, dass nur 2 und 3 auftauchen können als Primfaktoren (dank der Rekursion).
Es geht nur noch um die Anzahl der 2 und 3.
a1 interessiert nicht (verhindert nur, dass a(n-1) zu arg ins Gewicht fällt)
a2: einmal die 2
a3: einmal die 3
a4: zweimal die 2
a5: einmal die 2, einmal die 3
oder anders
a2: 1*a2 --> Anzahl 1
a3: 1*a3 --> Anzahl 1
a4: 2*a2 --> Anzahl 2
a5: 1*a2, 1*a3 --> Anzahl 2
a6: 2*a3 --> Anzahl 2
a7: 2*a3, 1*a3 --> Anzahl 3
a8: 1*a3, 2*a3 --> Anzahl 3
a9: 3*3a --> Anzahl 3
a10: 2*a2, 2*a3 --> Anzahl 4
a11: 1*a2, 3*a3 --> Anzahl 4
a12: 4*a3 --> Anzahl 4
a13: 2*a3, 3*a3 --> Anzahl 5
Die 3 schlägt die 2 (da höher). Man hat immer eine bestimmte Anzahl von Primfaktoren. Soweit man auf die 3 zurückgreifen kann, greift man auf die 3 zurück, ansonsten auf die 2. Das weotere ist einfach nur eine Permutation
Bildungsgesetz jetz leicht klarer für die explizite, nicht-rekursive Funktion?
Wieviele Faktoren (2,3) kommen zum Zuge? Wie oft kommt die 3 darin vor? Die übrigen sind 2en.
Also theoretisch dann einfach die 19702020 geteilt durch 3 und dann schauen was für ein Rest bleibt, wenn der Rest 2 ist gehts auch sofort auf, wenn der Rest eins is eine Drei weg und dafür zwei 2 dazu. Ist das dann die Lösung für die Aufgabe? Und wie kann ich beweisen, dass dieser Zusammenhang gilt? Danke :)
Der Beweis läuft sehr wahrscheinlich über vollständige Induktion. Beweise das einfach für n4,n5,n6 und dann für n(m+1), n(m+2), n(m+3)
Sieht gut aus. Vermutlich müsste man die Korrektheit dieses "offensichtlichen" Bildungsgesetzes auch noch beweisen. Wenn nicht, wäre es eine gute Übung ...
Hi, was meinst du mit Bildungsgesetz und wie könnte man diesen Beweis führen? :)
Der Code für VBA Excel, um sich die Zahlen anzugucken:
Sub x()
Dim l(1 To 100) As Long, lmax As Long
Dim i As Integer, n As Integer, d As Integer
i = 4
l(1) = 0
l(2) = 2
l(3) = 3
Cells(1, 1) = 0
Cells(2, 1) = 2
Cells(3, 1) = 3
For n = 4 To 55
lmax = 0
For d = 1 To n - 1
If l(d) * l(n - d) > lmax Then lmax = l(d) * l(n - d)
Next d
l(n) = lmax
Cells(n, 1) = lmax
Next n
End Sub
Ja, weil ich auf dem Arbeitsrechner kein C++ haben darf, auch kein Java, kein nichts, nur dieses VBA hat man mir nicht genommen.
Bei Excel hat man noch die schönen Tabellen, das hilft für Mathe-Aufgaben extrem und macht einiges wieder wett!
Ach, du Armer! Vielleicht ist das was für dich, wenn Excel mal nicht reicht: https://repl.it/languages
Bekomme ich ja alles nicht auf dem Arbeitsrechner installiert, ich habe keine Admnin-Rechte ...
Ich soll jetzt auch Massendatenanalyse-Tools mit VBA erstellen. Speicher ist voll, wenn es läuft, dauert es ewig, Bibliotheken funktionieren nicht wie man will (ADO, Dictionalry etc). …. macht kein Spaß ...
Musst du nicht installieren, läuft im Browser (der und Internet ist natürlich Voraussetzung).
Hiwi-Job oder richtige Anstellung? Wenn letzteres, schnell wechseln! Beruf ohne Spass sollte man sich nicht lange antun.
Ich arbeite als Wirtschaftsprüfer (und studiere nebenher gerade Informatik an der FU Hagen - ob das klappt mit Mathe, mega schwer …), die Arbeit macht eigentlich schon sehr viel Spaß, nur dieses Gefriemmel mit VBA klappt nicht gerade nicht so wie ich will.
Es soll eine Excel-Lösung für Prüfungszwecke herauskommen und bin jetzt nicht der VBA-Profi, lerne mich gerade in die höheren Themen ein. Und ich bin bös hintendran mit der Lösung.
Irgendwann soll es mit VBA flutschen (oder ich bekomme vielleicht irgendwann Java - Eclipse) und auch das dann Spaß machen, aufgeben will ich nicht, mit dem Arbeitgeber bin ich super glücklich, beim vorangegangenen hat mich der direkte Vorgesetzte (der mich nicht eingestellt hat) in Zusammenwirken mit drei miesen anderen Mitmobbern recht brutal rausgemobbt, deswegen bin ich hier wirklich mega froh!
Nach meinen Analysen hat kein Folgenelement den Primfaktor mehr als 2 mal, der Rest sind immer Dreien. Ich komme tatsächlich auf 6567340 Primfaktoren.
19702020 ist durch 3 teilbar ohne Rest (Quersumme ergibt 21, davon die Quersumme ist 3). Damit hätte ich vermutet, dass die 6567340 Primfaktoren nur 3 sind.
Ich verstehe leider Deine Herleitung im Bild nicht. Was war da genau die Logik?
Schon der Ausgangspunkt ist nicht gesichert, denn wer sagt, dass
a mit Index m aus dem Quadrat von a mit dem Index m/2 besteht (erster Schritt)? und nicht z.B. a_m = a_(m-2) * a(2) ??
Ich sehe in Deiner Vorgehensweise die max-Funktion nicht.
Statt dessen:
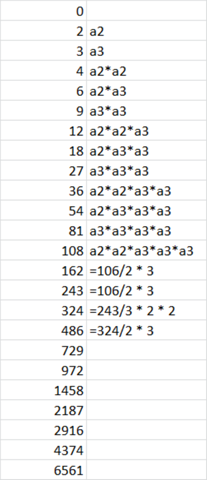
Also jetzt andere Rekursion-Vorschrift ohne max:
- wenn n mod 3 = 1 dann: a_(n+1) = a_n/3 * 2 * 2
- wenn n mod 3 ungleich 1: dann a_(n+1) = a_n/2 * 3
Und das versuche ich mal zu abstrahieren:
a4 = a3 / 3 * 2 * 2 = 4, passt
a5 = a4/ 2 * 3 = 6 und a6 = a5/2 * 3 = 9, passt.
Jetzt der Versuch für n+3 induktiv:
a_(n+3) und n mod 3 = 0: Wir nehmen aus der Annahme, dass a_n nur 3 als Primfaktoren hat. Als neue Faktoren hatte ich in einer anderen Antwort bzw. Kommentar bewiesen, dass a_(n+2) und a_(n+1) nicht für a_(n+3) genommen werden können, sondern frühestens a_n. Und da n durch 3 mit Rest teilbar ist, gehört als Counterpart a3 dazu. Da sich die Anzahl der Primfaktoren jedoch nur um1 in n-Dreierschritten erhöht (noch zu beweisen), muss a_n * a3 in diesem Fall das Maximum sein. Also besteht auch a_(n+3) nur aus 3, wenn n mod 3 = 0.
Jetzt der Beweis, dass sich die Primfaktoren um 1 erhöhen, wenn n sich um 3 erhöht. Das folgt aus der oben gezeigten Logik, dass zuerst die 2 durch die 3 ersetzt werden und wenn nur noch 3 vorhanden sind, wird die 3 durch 2*2 ersetzt.
Also versuche wir mal das zu beweisen. Schaffst Du den restlichen Beweis?
Nimm z.B. a5 bzw. a_(n+3) mit n mod 3 = 1. Wir gehen von der Annahme aus, dass a_(n+3) mit n mod 3 = 1 immer 2 Primfaktoren mit dem Wert 2 haben. Hier gilt, wie bereits bewiesen, es kommt frühestens a_(n+1) in Betracht (da a_(n+2) mit 0 zu multiplizieren wäre), jetzt aber mit Gegenpart a2 und das ist eine 2! Wir haben also eine 2 in dieser Kombination. Und jetzt checken wir a_(n+2). Für a_(n+1) gilt logischwerweise n+1 mod 3 = 2. Nach dem Induktionsannahme enthalten Elemente mit n+1 mod 3 = 2 einen Primfaktor mit 2. Dadurch erhöht sich die Anzahl der Primfaktoren auf 2. Und jetzt der Beweis, dass dies das Maximale ist. Das geht via 2² > 3 hoch 1.
Und zum Schluss noch für n mod 3 = 2, wobei man viel von oben verwenden kann, man muss aber aufpassen, dass keine Zirkelschlüsse eintreten.
Aber durchdenke es selbst, vielleicht liege ich irgendwo falsch!
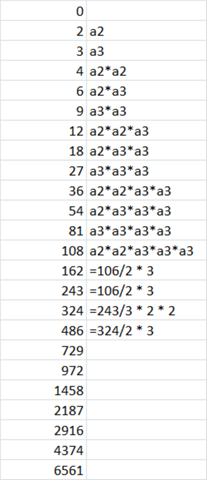
„Jetzt der Beweis, dass sich die Primfaktoren um 1 erhöhen, wenn n sich um 3 erhöht. Das folgt aus der oben gezeigten Logik, dass zuerst die 2 durch die 3 ersetzt werden und wenn nur noch 3 vorhanden sind, wird die 3 durch 2*2 ersetzt.
Also versuche wir mal das zu beweisen. Schaffst Du den restlichen Beweis?“
Mit konkreten Zahlenbeispielen habe ich das ganze jetzt gezeigt, aber ich glaube nicht dass das einen Beweis darstellt :/ Wie könnte man des ganze allgemein für a_n zeigen? :)
Versuche, eine allgemeine Beziehung zwischen a_n und dem jeweils dritten Nachfolger herauszufinden, also a_(n+3). Diese Struktur ist dann allgemein gültig, gilt für die gesamte Folge.
Man sollte aber wie gesagt drei Fälle unterscheiden, je nach dem, was als Rest herauskommt, wenn man n durch 3 teilt. Dann hast Du 3 Fälle. Und für jeden dieser dreien einen Beweis und dann hast Du es.
In meiner Tabelle oben siehst Du: zuerst wird ein a2 durch ein a3 ersetzt. Dann wird das zweite und letzte a2 durch a3 ersetzt, dann sind nur noch a3 da. Als nächstes wird ein a3 durch 2 a2 ersetzt und es wiederholt sich.
Ich sehe gerade: Es gilt allgemein ab n größer gleich 5:
a mit Index (n) = a mit Index (n-3) * a3 (also mal 3)
Das ist nochmals eine kürzere Rekursionsformel als bisher.
Bekommst Du das allgemein gültig bewiesen? Es kommt einfach immer eine 3 dazu im Vergleich zum drittvorangegangsten. Für n bis 5 muss man es ausrechnen, das gilt dann als gegeben.
Ich muss jetzt abdüsen, morgen wieder
Ich bin davon ausgegangen, dass man den maximalen Wert erhält, wenn man n/2 mit n/2 multipliziert, ich glaube, da liegt mein Fehler, oder?
Ja, das ist definitiv nicht zwingend, und entsprechend meinen Analysen in den meisten Fällen falsch.
In der Regel wird der maximale Wert mit dem äußersten Klammerpaar berechnet, also mit n-2 mal 2 oder n-3 mal 3 (also zum Beispiel: Sie n = 10002. Dann ist a_n = a_(n-3) * a_3, so mein "Beweis" - in Anführungszeichen, weil noch nicht ganz rund). Das habe ich oben zu beweisen versucht. Das äußerste Klammerpaar erzwingt auch die Struktur, denn bei n-2 kommt die 2 hinzu und bei n-3 die 3.
Also nochmal zu deiner hergeleiteten Formel, dass die Gesamtzahl der Primfaktoren sich mit (n-1)/3 + 1 berechnen lässt: Ich hab verstanden dass jeweils nach 3n ein zusätzlicher 3er als Primfaktor hinzukommt; aber wieso ziehst du vom n erst eins ab und rechnest danach zur Gesamtzahl eins dazu?
Das war nur zum Runden in Excel. Der Abzug ist ja vor dem Teilen durch 3, das plus 1 danach.
wenn n= 2 oder n = 3, dann ein Primfaktor
wenn n von 4 bis 6, dann zwei Primfaktoren,
wenn n von 7 bis 9, dann drei Primfaktoren
usw
Daraus habe ich die Formel abgeleitet Ganzezahl von ((n-1)/3 + 1). Das +1 hilft nur zum Aufrunden. Das minus 1 verschiebt den Index, weil 3/3 + 1 sonst 2 ergäbe.
ah, die n-1 liegt daran, dass a_1 noch keinen Primfaktor hat, oder? Aber warum zählst du am Ende nochmal einen Primfaktor dazu?
das -1 ergibt sich aus der Notwendigkeit der Verschiebung. Links der Index, rechts die Anzahl der Primfaktoren.
1 --> 1
2 --> 1
3 --> 1
4 --> 2
5 --> 2
6 --> 2
7 ---> 3
usw.
Das -1 dient einfach dazu, die linke Seite eins nach oben zu verschieben, dass die 1 zur 0 wird, die 2 zur 1, die 3 zur 2 usw. Wenn ich jetzt durch 3 teile, bekomme ich einen Wert kleiner 1 (für die ersten 3, für 4-6 bekomme ich einen Wert zwischen 1 und 2, für 7-9 einen Wert zwischen 2 und 3 usw). Das kann ich jetzt entweder aufrunden, um die Zahl der Primfaktoren zu erhalten, und wäre fertig, oder - da Excel nur abrundet - ich zähle 1 dazu und runde dann ab und erhalte so für 1-3 die 1, für 4-6 die 2, für 7-9 die 3 usw.
Es ist einfach nur ein Trick, den man in der Programmierung häufig anwendet, keine wirkliche Logik der Mathematik.
Du hast a1, a2 und a3 gegeben.
Nun musst du (als nächstes) a4 berechen.
dazu lässt du d von 1 bis 3 "laufen" und berechnest:
für d=1: a1*a3
für d=2: a2*a2
für d=3: a3*a1
von diesen (in dem Fall) 3 Werten nimmst du den größten (Maximum) und du hast dein a4.
für a5 lässt du d von 1 bis 4 laufen, u.s.w.
So, jetzt habe ich die Bildungsvorschrift:
Es gibt immmer (n-1)/3 +1 Primfaktoren
wenn n mod 3 = 0, gibt es kein 2er Primfaktor
wenn n mod 3 = 2, dann gibt es einen 2er Primfaktor
wenn n mod 3 = 1, dann gibt es zwei 2er Primfaktoren
Das übrige sind die 3er.
Wenn ich als weiter nachdenke, bekomme ich vielleicht irgendwann den Beweis.
genial :) könntest du vielleicht mir kurz beschreiben, wie du auf die annahme gekommen bist, es gibt immer (n-1)/3 + 1 Primfaktoren?
Indem ich den Code (in einer anderen Antwort) in Excel eingegeben und dann die Ergebnisse analysiert habe.
Die 2er Primfaktoren tauchen immer in der Reihenfolge auf 1-0-2, 1-02. Die Gesamtzahl der Primfaktoren nimmt nach jeweils 3 n zu. Logisch, weil es ja durch-permutiert: Wir haben z.B. die Anzahl m. Drei Folgemitglieder haben m Primfaktoren, sagen wir z, z+1, z+2
Dann hat z den geringsten Wert mit zwei 2en, das nächste Folge-Mitglied z+1 hat nur noch eine 2, dafür eine 3 mehr. Und z+2 hat keine 2, dafür zwei 3en mehr. Und dann geht es mit m+1 Primfaktoren weitern.
Beweis-Überlegungen: n4 kann zum ersten Mal auf 2 Primfaktoren zurückgreifen, n5 kann das auch, allerdings kann es sich eine 3 schnappen, n6 kann sich zwei 3en schnappen. n5 kann sich nämlich die 3 aus n3 (=n5-2) nehmen, n6 kann auf die 3 aus n3 (n6-3) und n5 (n6-1) zurückgreifen.
Das läuft also über einen Beweis der vollständigen Induktion.
Ich habe das ganze jetzt einfach versucht mal händisch aufzulösen durch Rechnen, ich füg das Bild der Frage hinzu, da ich hier kein Bild anfügen kann.
Ja, sehr schön. Und jetzt das abstrakte Bildungsgesetz via Induktion beweisen, dann werden die Zusammenhänge klarer. Wenn ich dazu komme, versuche ich es auch einmal.
Es ist vielleicht einfacher, von unten anzufangen, um das für die Induktion relevante Induktionsmuster zu erkennen.
Leider hatten wir in der Schule noch keine Beweisführung oder ähnliches (Gymnasium 11. Klasse); das sind Aufgaben die wir von unserem Lehrer über die Ferien zum Lösen bekommen haben und den Beweis der Lösung danach in einem kurzen Referat der Klasse vorstellen sollen :/
Alter Schwede, so was in der 11. Klasse!
Der Induktionsbeweis geht wie folgt: Du versuchst erst einmal a4, a5, a6, a7, vielleicht bis a12 über a mit einem niedrigeren Index darzustellen (das ist noch nicht der Beweis, sondern die erste Analyse).
Wir behaupten und weisen unmittelbar nach
a4, a5, a6 haben nur zwei Primfaktoren.
Jetzt behaupten wir, dass a(4 + 3*n), a(5+3*n), a(6+3*n), n Element natürliche Zahlen zwei + n Primfaktoren haben.
Das beweisen wir wie folgt: Da es immer ein Produkt aus einem anfänglichen Element und einem späteren Element sein muss, haben alle Produkte desjeweiligen a_n dieselbe Anzahl von Faktoren mit maximaler Abweichung von 1.
Die Faktorkombination a(n-1) * a1 kann nicht die maximale sein, da a1 0 ist. Also kommen nur die Faktoren a(n-2) bis a2 in Betracht.
a(n-2) hat nur dann gleich viele Faktoren wie a(n), wenn a(n-2) zweimal die 2 in der Primfaktorzerlegung hat, dann kommt aber mit a2 eine dritte 2 hinzu. Und 2 hoch 3 ist 8, weniger als 3 hoch 2. Damit scheidet auch a(n-2) aus. Damit kommt nur noch a(n-3) * n3 in Betracht als erste Maximalgröße. Dieses n-3 zeigt schon klar die 3-Schritte.
a(n-3)*a3 muss sich jetzt mit a(n-4) * a4 messen lassen. Und auch hier wieder die Strukturunterschiede ausmachen. Entweder a(n-4)*a4 hat bereits die maximale Anzahl von 3 oder wir gehen runter auf a(n-5)*a5. Es gilt immer: Wir können auf einen Primfaktor 2 verzichten, wenn dafür die 3 Zweien gegen 2 dreien getauscht werden, da 3² > 2³.
Und so weiter analysieren, bis der Beweis abstrakt sitzt und ein Muster ersichtlich wird.
Danke, das muss ich jetzt erstmal durchblicken :)
Ich habe grad nochmal bisschen gerechnet und die Formel von oben ausprobiert und geschaut wie die zu meinem errechneten Ergebnis passt.
Du hast vorhin festgestellt, dass es (n-1)/3 +1 Primfaktoren gibt. Nach meinem errechneten Ergebnis komme ich aber auf rund 400 000 Primfaktoren mehr, ich verstehe irgendwie nicht, woran das liegt vielleicht habe ich irgendwo einen Rechenfehler. Nach deiner Formel würde ich aber auf ...,67 Primfaktoren, wie soll ich das verwerten?
Auch haben wir ja vorhin festgestellt dass sich die dreier als Primfaktoren immer durschlagen, aber ich habe ja jetzt mehr zweier als dreier.
Ich weiß jetzt nicht wo ich mich verrechnet habe oder gerade einfach einen Denkfehler; würde mich freuen wenn du mir vielleicht sagen könntest, woran es liegt :)
Nach meinen Analysen hat kein Folgenelement den Primfaktor mehr als 2 mal, der Rest sind immer Dreien. Ich komme tatsächlich auf 6567340 Primfaktoren.
19702020 ist durch 3 teilbar ohne Rest (Quersumme ergibt 21, davon die Quersumme ist 3). Damit hätte ich vermutet, dass die 6567340 Primfaktoren nur 3 sind.
Ich verstehe leider Deine Herleitung im Bild nicht. Was war da genau die Logik?
Schon der Ausgangspunkt ist nicht gesichert, denn wer sagt, dass
a mit Index m aus dem Quadrat von a mit dem Index m/2 besteht (erster Schritt)? und nicht z.B. a_m = a_(m-2) * a(2) ??
Ich sehe in Deiner Vorgehensweise die max-Funktion nicht.
Ich setze mal eine neue Antwort
Hi, vielen Dank für deine Antwort :) Am größten ist dann also immer das Paar in der Mitte, oder? Aber wie Komme ich dann auf a19702020, ohne alle Schritte vorher durchzumachen? Auf eine explizite Beschreibung, wie du meintest komme ich irgendwie gerade nicht, ich stehe da etwas auf dem Schlauch :/
Danke für deine Hilfe :)