Matheaufgabe Leuchtturm - wie würdet ihr die Aufgabe lösen?
Hallo. Ich habe folgende Mathehausaufgabe bekommen: Ein Schiff peilt einen Leuchtturm unter einem Winkel von 87 ° zur Fahrtrichtung an. Nach einer Fahrststrecke von 5400 Metern wird ein Winkel von 110 ° gemessen. Wie weit war das Schiff in beiden Punkten vom Leuchtturm entfernt? Wie würdet ihr die Aufgabe lösen?
8 Antworten
Die Höhe des Leuchtturms ist bei diesem Beispiel absolut uninteressant. Du benötigst zur Lösung dieses Beispiels die trigonometrischen Formeln fü rechtwinklige Dreiecke (hier: tanα = GK/AK)
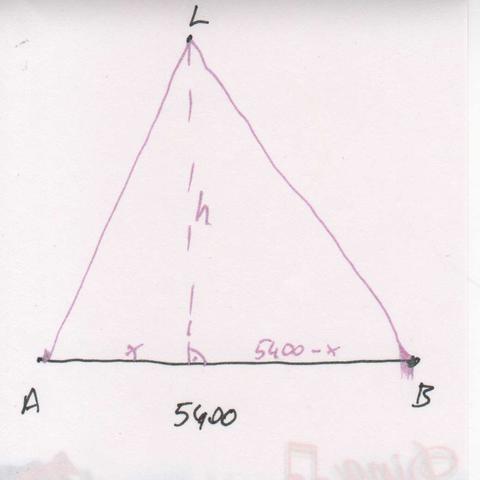
Im beigefügten Bild siehst du die Skizze: L...Leuchtturm, A...erster Messpunkt, B....zweiter Messpunkt; ∡LAB=87°, ∡LBA=70°
Rechenweg:
Gesucht ist:
- AL = √(h²-x²)
- BL = √(h²+(5400-x)²)
- ⇒ du hast zwei Unbekannte; diese errechnest du mit Gleichungssystem:
- I: tan87 = h/x ⇒ h=x·tan87II: tan70 = h/(5400-x) ⇒ h = (5400-x)·tan70
- Jetzt diebeiden rechten Seiten gleichsetzen:x·tan87 = (5400-x)·tan70 ⇒ x = 679,68
- x einsetzen in "h=..."
- jetzt x und h einsetzen in "AL=.." und "BL=..." und du hast die gesuchten Antworten.
Falls ihr schon Berechnungen am allgemeinen Dreieckgelernt habt, geht es mit dem Sinussatz einfacher:
- LB/sin87 = 5400/sin23 (der √ABL=23° ergibt sich aus den beiden bekannten Winkel!) ⇒ LB = 5400·sin87/sin23
- LA/sin70 = 5400/sin23 ⇒ LA = 5400·sin70/sin23
Du hast ein Dreieck mit der Seite 5400m, einem Winkel von 87 Grad und auf der anderen Seite einem Winkel von 70 Grad (180 - 110). Der dritte Winkel ist also 23 Grad. Mit diesen vier Angaben ist das Dreieck eindeutig bestimmt, Sinus- bzw. Kosinussatz erledigen den Rest.
Die WINKELFUNKTIONEN sin, cos, tan und cot gelten im rechtwinkeligen Dreieck. SINUSSATZ und COSINUSSATZ gelten für das allgemeine Dreieck.
Ganz einfach:
Zunächst hast du eine Entfernung von 5400+x und dann von x da er beim zweiten Punkt 5400 Meter näher am Turm ist.
Dann hast du noch die Höhe h des Leuchtturmes, die wir zwar nicht kennen aber die wir gleich noch brauchen werden.
Anmerkung: Es ist ja jetzt von dir der Winkel an der Leuchtturmspitze gegeben, so wie ich das verstanden habe. Deswegen wird aus den 110° erst mal 70°, da in einem rechtwinkligen Dreieck (der rechte Winkel ist der am Boden des Leuchtturmes) die beiden anderen Winkel jeweils kleiner als 90° sind, weil alle Winkel zusammen immer 180° ergeben müssen und weil im Einheitskreis gleichwertig sind. (sin(70°) = sin(110°) als Beispiel ABER tan(70°) = -tan(110°)).
Jetzt ist der erste Winkel, der bei 5400+x gemessen wird 87°.
(5400+x)/h = tan(87°)
Der zweite Winkel ist 20°
Wenn unser Schiff jetzt 5400 Meter weiter gefahren ist, beträgt seine Distanz zum Leuchtturm per Definition genau x.
x/h = tan(110°)
Jetzt können wir einfach beide Brüche also h/(5400+x) und h/x mit einander Teilen, damit sich die Höhe vom Leuchtturm herauskürzt.
(x/h)/((5400+x)/h) = tan(70°)/tan(87°)
<=>x/(5400+x) = tan(70°)/tan(87°)
<=>x = (x+5400)*tan(70°)/tan(87°)
<=>x= x*tan(70°)/tan(87°) + 5400*tan(70°)/tan(87°)
<=>5400*tan(70°)/tan(87°) = x - x*tan(70°)/tan(87°)
<=>5400*tan(70°)/tan(87°) = (1-tan(70°)/tan(87°))*x (einfach x ausklammern)
<=>5400*tan(70°)/tan(87°)/(1-tan(70°)/tan(87°)) = x
Wenn du jetzt die ganzen Tangens einheitlich zusammenschreibst kommst du auf x = 5400*tan(70°)/(tan(87°)-tan(70°)) = 908.331
Erste Distanz: 5400m + x = 5400m + 908.331m = 6308.331m
Zweite Distanz x = 908.331m
Antwort: Beim ersten Punkt war das Schiff noch 6308.331m und beim zweiten Punkt 908.331m vom Leuchtturm entfernt.
Ich hoffe ich konnte dir helfen! :)
JTR
Shit, mir ist ein kleiner Fehler ganz am Ende unterlaufen:
Der Winkel Beträgt ja beim zweiten Punkt 110°, was ja -70° entspricht. Das heißt, dass das Schiff beim zweiten Punkt HINTER dem Leuchtturm aber beim ersten Punkt noch DAVOR ist, weswegen du für die erste Distanz nicht 5400+908.331 sondern 5400 - 908.331 = 4491.669 rechnen musst.
Deswegen beträgt die erste Distanz 4491.669m.
Sorry!
Ohne Sinus- und Kosinussatz:
Sei A der erste Standort und B der zweite. Der Fußpunkt des Lots
von Leuchtturm L auf die Gerade AB sei F und seine Länge sei d.
AB = a = 5,4 km und BF = b.
Dann ist tan α = d / (a + b) → a + b = d / tan α und tan ß = d / b → b = d / tan ß.
Also ist (a + b) / b = tan ß / tan α → a/b + 1 = tan ß / tan α →
a/b = tan ß / tan α ‒ 1 = (tan ß - tan α) / tan α → b/a = tan α / (tan ß - tan α) →
b = a tan α / (tan ß - tan α). Damit ist AL = (a + b) / cos α und BL = b / cos ß.
Ich würde es mit Trigonometrie lösen, falls ihr das schon hattet.
Da müsste man aber auch eine Länge haben...
Oder möglicherweise auch mit Ähnlichkeit.
Aber ich dachte, Sinus/Kosinus/Tangenz gelten nur im rechtwinkligen Dreieck? Das hier ist aber kein rechtwinkliges.