Mathe ich brauche Hilfe beim Aufgabe 9?

Answer 1

[MichaelH77]

man verwendet als Ansatz die Punkt-Steigungsform der Tangenten

f(u)=f'(u)*(u-x)+y

bei x und y setzt man die Koordinaten des gegeben Punkts ein, bei f(u) die Funktion und bei f'(u) deren Ableitung:

$-\frac{1}{2}u^3+\frac{3}{2}u+2=\left(-\frac{3}{2}u^2+\frac{3}{2}\right)\left(u-2\right)+5$ löst man diese Gleichung nach u auf, dann erhält man die x-Werte der Berührpunkte

u=0 und u=3

mit diesen u wird f'(u) berechnet und in obige Formel eingesetzt, x und y wieder vom gegeben Punkt

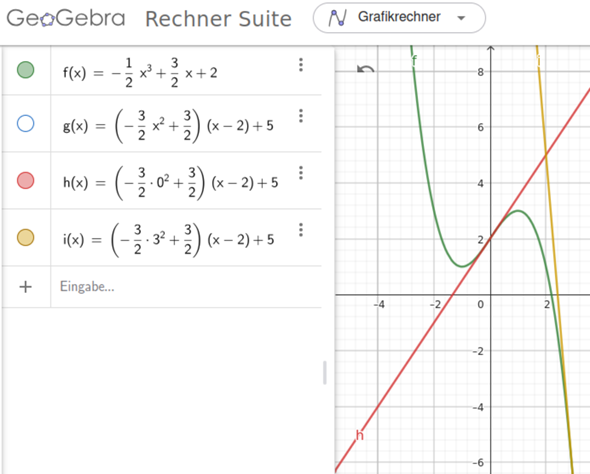
die erste Tangente lautet dann y=f'(0)*(x-2)+5
die zweite Tangente y=f'(3)*(x-2)+5

die Tangentensteigungen können als Zahl berechnet werden und dann die klammer ausmultipliziert und zusammengefasst um die typische Geradengleichung zu erhalten

Comments

[Halbrecht]

mal was anderes : weißt du , wie man bei Geogebra Fkt nur in einem Intervall anzeigen lassen kann ?

[MichaelH77]

@Halbrecht

z.B. f(x)=x², (0<x<5) oder mit dem Wenn Befehl oder funktion(gleichung,startwert,endwert)

[Halbrecht]

@MichaelH77

so günstig kann einfach sein . Danke ! Klappt

Endlich Viertelkreise

Answer 2

[Halbrecht]

bestimme zuerst f'(x)