LGS mit Gauß verfahren?
hey, ich bräuchte Hilfe bei meiner Matheaufgabe die lautet:
a) Gesucht ist eine ganzrationale Funktion dritten Grades mit dem Tiefpunkt P (1/-2), deren Wendepunkt im Koordinatenursprung liegt.
Ich weiß nicht wie man die lösen muss, ich hoffe jemand kann helfen.
3 Antworten
LGS mit Gauß verfahren?
Das wäre mit Kanonen auf Spatzen geschossen.
Schon wenn man liest "Ursprung" kann man sich freuen, dass vieles zu Null wird und das LGS dadurch vereinfacht wird.
Ansatz:
f(x) = ax^3 + bx^2 + cx + d
f'(x) = 3ax^2 + 2bx + c
f' '(x) = 6ax + 2b
Und als erstes nehmen wir die Aussagen zum Ursprung:
f(0) = 0
d = 0
f' '(0) = 0
b = 0
Bleibt also:
f(x) = ax^3 + cx
f'(x) = 3ax^2 + c
f'(1) = 0
3a + c = 0
c = -3a (1)
f(1) = -2
a + c = -2 (2)
(1) in (2)
a - 3a = -2
-2a = -2
a = 1
c = -3a = -3
Lösung:
f(x) = x^3 - 3x
und das sieht so aus:
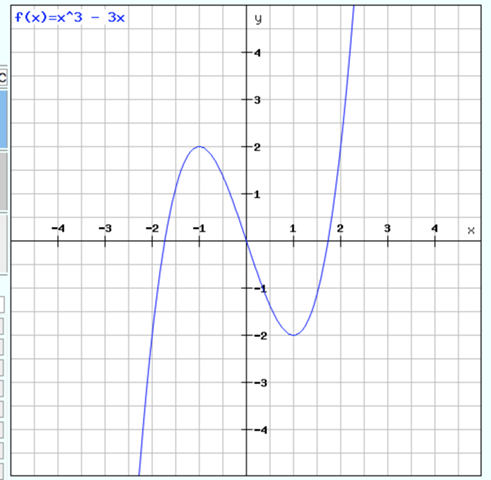
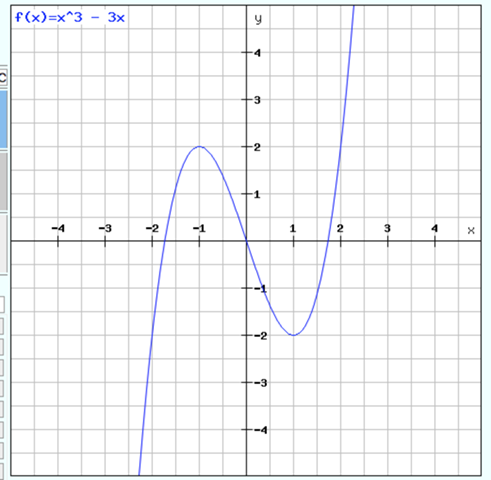
Vier Bedingungen sind da
.
f(1) = 2
f'(1) = 0
f(0) = 0
f''(0) = 0
.
Daraus entstehen
-2 = a + b + c + d
0 = 3a + 2b + c
0 = d.........................d schon da
0 = 0 + b
hieraus ......b = 0 ..........b ist schon da
.
Einsetzen in die Glg , die noch da sind
-2 = a + c >>>>> c = -2 -a ....einsetz
0 = 3a + c
0 = 3a + (-2-a)
0 = 3a -2 -a
+2= 2a......................a = 1
.
-2 = 1 + c
-3 = c
.
f(x) = 1x³ + 0x²- 3x + 0
f(x) = x³ - 3x
.
PS Was meinst du mit Gauß ?
Hallo,
der Wendepunkt einer kubischen Funktion ist gleichzeitig deren Symmetriezentrum.
Wenn er bei (0|0) liegt, handelt es sich um eine ungerade Funktion, bei der die Variable nur in ungeraden Potenzen vorkommt.
Schema: f(x)=ax³+bx.
Du brauchst also nur a und b zu bestimmen.
Herzliche Grüße,
Willy