Matheaufgabe: bestimmen Sie eine ganzrationale Funktion mit angegebenen Eigenschaften?
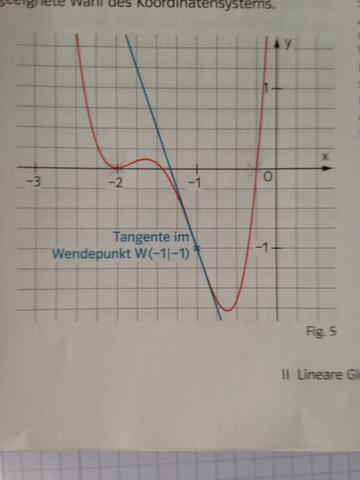
Hallo ihr! Die Aufgabenstellung lautet: Bestimmen Sie eine ganzrationale Funktion 4. Grades, deren Graph die in Fig. 5. angegebenen Eigenschaften hat. Also, mit dieser Aufgabe habe ich ein paar Schwierigkeiten, um normale Punkte, Wendepunkte, Sattelpunkte oder Hoch- und Tiefpunkte zu ermitteln. Es wäre super, wenn ich vernünftige Angaben bekommen könnte, da mir das in meiner Note helfen könnte. Ich bin jedem Dankbar der hilft!
3 Antworten
Du weißt vom Funktionsgraphen her, dass eine doppelte Nullstelle bei x=-2 vorliegt, weitere Nullstelle ist bei x=-0.25
Weiterhin sagt Dir die Form, dass es sich um eine Funktion 4. Grades handelt.
Der Funktionsterm ist also (x+2)² * (x+0.25) * (x + a)
Das a gilt es noch zu bestimmen, auch das ist nicht weiter schwer, wenn Du berücksichtigst, dass f(-1)=-1.
f(-1) = 1² * 0,75 * (-1+a)
Die Angabe des Wendepunkts kannst Du dann als zur Überprüfung des Ergebnisses nutzen.
Hinweis: x = -1/4 ist keine Nullstelle von f. Leider ist die Darstellung in der Grafik missverständlich.
Quelle: Lambacher Schweizer, Mathematik für Gymnasien, Kursstufe, Baden-Württemberg, S. 229 Nr. 12
f(x) = ax^4+bx³+cx²+dx+e
f '(x) = 4ax³+3bx²+2cx+d
f ''(x) = 12ax²+6bx+2c
I. f(-2) = 0 ... Nullstelle bei x = -2
II. f(-1) = -1 ... W(-1 | -1)
III. f '(-2) = 0 ... Extremstelle bei x = -2
IV. f ''(-1) = 0 ... Wendestelle bei x = -1
V. f '(-1) = -3 ... Steigung der Wendetangente ist -3
I. 16a - 8b + 4c - 2d + e = 0
II. a - b + c - d + e = -1
III. -32a + 12b - 4c + d = 0
IV. 12a - 6b + 2c = 0
V. -4a + 3b - 2c + d = -3
Der GTR liefert die Lösungen dieses LGS:
a = 3, b = 17, c = 33, d = 24, e = 4
Also ist die gesuchte Funktionsgleichung gegeben durch
f(x) = 3 x^4 + 17 x³ + 33 x² + 24 x + 4.
...................
Die Nullstelle in der Nähe von -1/4 ist übrigens -5/6+(1/6)*sqrt(13), also ungefähr -0,2324081207.
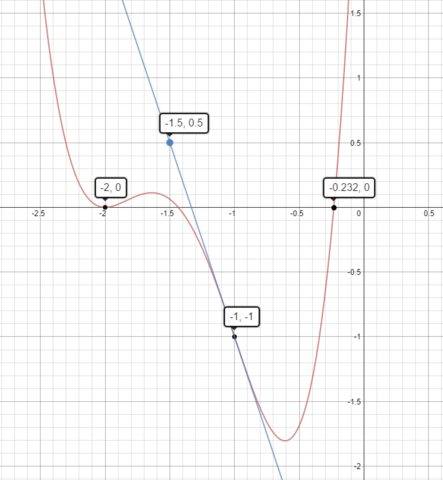
Ansatz ähnlich wie Mikkey, aber f(x) = a(x + 2)²(x + ¼)(x + b)
Wp. (- 1 | - 1) gibt f(- 1) = - 1 und f´´(- 1) = 0
und Steigung der Wendetangente f´(- 1) = - 3
Keine Nullstelle bei x = -1 / 4. (laut Lösungsbuch)
Zudem ist das LGS mit den 6 Bedingungen
f(-2) = 0,
f '(-2) = 0,
f(-1/4) = 0,
f(-1)=-1,
f '(-1) = -3,
f ''(-1) = 0
nicht lösbar.
Du hast den Streckungsfaktor vergessen.
Die Funktionsgleichung lautet
f(x) = b * (x+2)² * (x+0.25) * (x + a).