Kann mir jemand bei dieser Mathe Aufgabe helfen?

Kann mir jemand erklären wie ich das Schritt für Schritt rechne? Ich verstehe es einfach nicht

Answer 1

[indiachinacook]

Das Ding besteht aus zwei einfachen geometrischen Figuren, nämlich einer Pyramide und einen Zylinder. Von beiden kann man getrennt die Volumina berechnen:

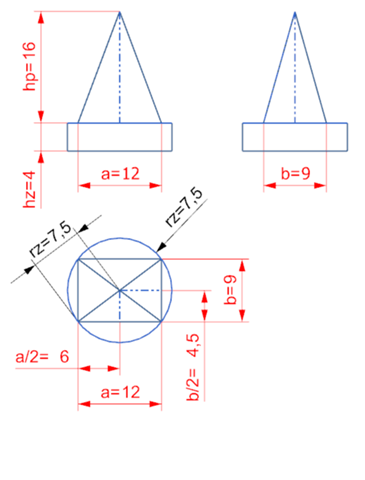
• Die Pyramide hat eine rechteckige Grundfläche mit Seiten a und b, und die Höhe hₚ. Das Volumen ist bekanntlich Grundfläche×Höhe durch Drei, also Vₚ=​⅓abhₚ=​576 cm³
• Der Zylinder hat ein Volumen von Grundfläche×Höhe. Die Grundfläche ist ein Kreis, dessen Durchmesser genau der Diagonale des Rechtecks entspricht, d=½√(a²+b²)=15 cm, der Radius ist die Hälfte davon, und die Flache ist natürlich r²π. Also ist das Volumen Vₓ=r²πhₓ=¼(a²+b²)πhₓ≈707 cm³
• Das Gesamtvolumen ist die Summe, also ungefähr 1283 cm³

Answer 2

[merkurus]

Berechnung
---
Pyramide Volumen Vp
Geg.: a = 12 cm ; b = 9 cm ; hp = 16 cm
Ges.: Vp
---
Vp = a * b * hp / 3
Vp = 12 * 9 * 16 / 3
Vp = 576 cm³
---
Zylinder Volumen Vz
Vz = rz² * pi * hz
Vz = 7,5^2 * pi() * 4
Vz = 706,858347 cm³
---
Gesamtkörper Volumen V
V = Vp + Vz
V = 576 + 706,858347
V = 1282,858347 cm³