Kann mir einer die Herleitung erklären, warum wenn in der Koordinatenform zum Beispiel die x3 Komponente fehlt, die Ebene parallel zu x3 Achse ist?
2 Antworten
Die unendlich vielen Koordinatentripel (x1, x2, x3) die die Koordinatengleichung erfüllen (sodass sie also wahr ist und nicht 0=1 o.ä. rauskommt) bilden die Ebene.
Weil die Gleichung die die Ebene beschreibt für jedes beliebige x3 erfüllt ist, ist x3 für jedes Koordinatenpaar (x1, x2) beliebig wählbar. Daraus folgt, dass der Normalenvektor der Ebene nicht in x3-Richtung zeigt, die Ebene ist also parallel zur x3-Achse.
Oder: Die Koeffizienten vor den Koordinaten bilden den Normalenvektor. Kein x3 bedeutet also 0*x3, also ist die x3-Komponente des Normalenvektors 0.
Weil dann x_3 keinen Einfluss hat, ob der Punkt in der Ebene liegt. Wenn also ein Punkt in der Ebene liegt, dann liegen auch alle anderen Punkt mit anderen x_3-Koordinaten in der Ebene, also alle Punkte entlang der x_3-Achse. Somit ist die Eben parallel zu dieser.
Mit der Ebenengleichung
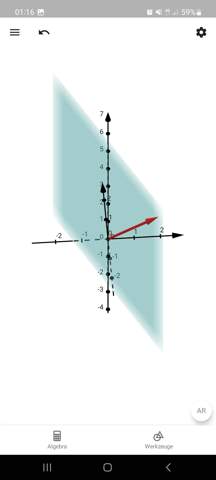
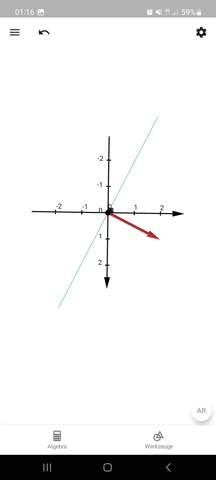
x_1 + 2 x_3 = 0,
also dem Normalenvektor (1, 2, 0), sieht es so aus (Normalenvektor in rot):
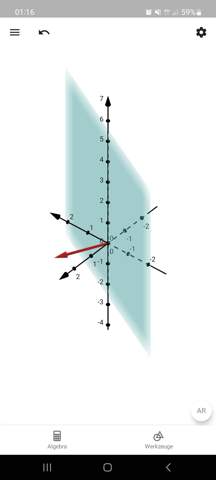
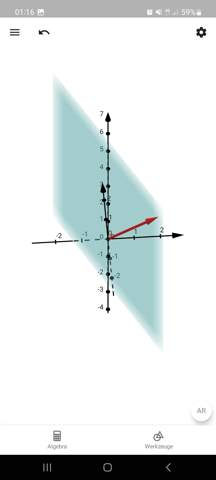
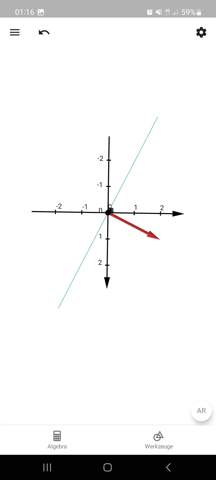

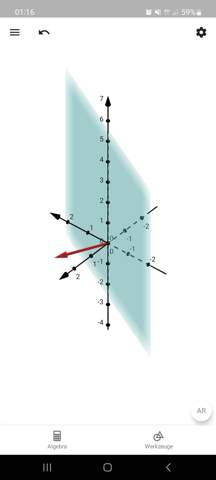

Also die Ebene zeichnet man ja mit den Spurpunkten ein, aber wie ist das Vorgehen beim Einzeichnen des normalenvektors?
Also gehe ich sozusagen, wenn ich ihn einzeichnen möchte, beim normalen Vektor 1/ 2 /0
1 in X1 Richtung um dann 2 in X2 Richtung. Dann komme ich ja beim Punkt an und dann verbinde ich mithilfe eines Pfeils vom Ursprung zu diesem Punkt, welcher dann der normalen Vektor ist, richtig?
Ja
Danke!
wie wäre der Normalenvektor zb (1/2/0) im Koordinatensystem eingezeichnet
Kann mir vorstellen wie die Ebene aussieht aber nicht wie der normalen Vektor aussieht und in welche Richtung der zeigt
er steht ja senkrecht auf der Ebene
Also gehe ich sozusagen, wenn ich ihn einzeichnen möchte, beim normalen Vektor 1/ 2 /0
1 in X1 Richtung um dann 2 in X2 Richtung. Dann komme ich ja beim Punkt an und dann verbinde ich mithilfe eines Pfeils vom Ursprung zu diesem Punkt, welcher dann der normalen Vektor ist, richtig?