Kann jemand die Aufgaben lösen?

Answer 1

[merkurus]

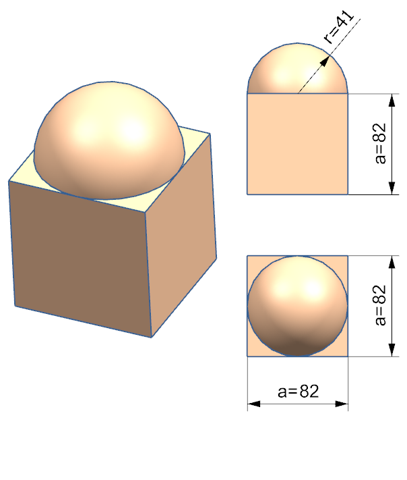
Aufgabe 6b
Volumen Halbkugel V1
V1 = (4/3 * pi * r³) / 2
V1 = (4/3 * pi() * 41^3) / 2
V1 = 144347,804852 cm³
---
Volumen Würfel V2
V2 = a³
V2 = 82^3
V2 = 551368 cm³
---
Gesamtkörper Volumen V
V = V1 + V2
V = 144347,804852 + 551368
V = 695715,804852 cm³
------------
Oberfläche Halbkugel O1
O1 = (4 * pi * r²) / 2
O1 = (4 * pi() * 41^2) / 2
O1 = 10562,034501 cm²
---
Oberfläche Würfel O2
(6 Quadrate)
O2 = 6 * a²
O2 = 6 * 82^2
O2 = 40344 cm²
---
Fläche Kreis A1
A1 = r² * pi
A1 = 41^2 * pi()
A1 = 5281,017251 cm²
---
Oberfläche Gesamtkörper O
O = O1 + O2 - A1
O = 10562,034501 + 40344 - 5281,017251
O = 45625,01725 cm²

Answer 2

[Tannibi]

Wo hakt es denn

Comments

[MaxBeck23443]

Aufgabe b

[Tannibi]

@MaxBeck23443

MAchst du genauso wie a, nur mit Quader statt Zylinder.

Answer 3

[daCypher]

Ich schätze mal, dein Problem ist die Oberfläche vom rechten Körper, oder?

Beim Würfel hast du fünf Seiten, die du ganz normal berechnen kannst. Die Oberfläche der Halbkugel kannst du auch ganz normal berechnen.

Dazu kommen jetzt nur noch die Ecken der oberen Seite vom Würfel, die nicht von der Halbkugel überdeckt werden. Das ist aber einfacher, als es aussieht. Du rechnest einfach die ganze Oberseite des Würfels (82*82) und ziehst davon den Kreis ab, der von der Halbkugel überdeckt wird, also 41²π.

Answer 4

[Karacho158]

Wenn du es nicht verstehst: dafür ist Unterricht ja da.

Das eine ist ein Zylinder mit einer halben Kugel oben drauf.

Das andere ein Würfel mit einer halben Kugel.