Exponentialfunktionen: Wie berechne ich den Flächeninhalt der von der Funktion, seiner Tangente und der Geraden eingegrenzte Fläche?
Guten Abend, wie in meiner Frage schon deutlich wird, geht es im Bereich der Exponentialfunktionen um eine Flächeninhaltberechnung einer eingegrenzten Fläche. Ich schreibe morgen eine Mathe-Klausur über dieses Thema und bin im Buch beim Üben über eine Aufgabe gestolpert die genau das fordert.
Ich kenne die einzelnen Komponenten, aber habe überhaupt keinen Anhaltspunkt wie ich anfangen soll. Vielleicht kann mir jemand einen Tipp geben!
Die Aufgabe ist im Anhang!
MfG

3 Antworten
Hallo,
zunächst mußt Du die Tangente an f(0) berechnen. Sie ist eine Gerade, die dieselbe Steigung hat wie die Funktion bei x=0 und zu der der Punkt (0|2) gehört.
Die Steigung rechnest Du über die Ableitung f'(x) aus. Für f(x)=e^x+1 ist f'(x)=e^x. f'(0) ist dann 1, denn irgendetwas hoch Null ist immer 1. Nur bei 0^0 ist das eine Sache der Definition - der Fall betrifft uns hier aber nicht.
Also gilt für die Tangentengleichung: y=x+b. b muß 2 sein, damit der Punkt (0|2) auf der Geraden liegt, also g(x)=x+2.
x=-4 ist einfach die untere Integrationsgrenze, die obere ist 0, weil f(x) und g(x) sich bei Punkt (0|2) schneiden.
Du mußt also das Integral von f(x)-g(x) bilden und in den Grenzen
von -4 bis 0 integrieren.
Also h(x)=e^x+1-x-2=e^x-x-1
Dann ist H(x)=e^x-x²/2-x
H(0)=1
H(-4)=e^-4-8+4=-3,982 (gerundet)
1-(-3,982)=4,982 Flächeneinheiten.
Ich lade Dir eine Skizze hoch.
Herzliche Grüße,
Willy
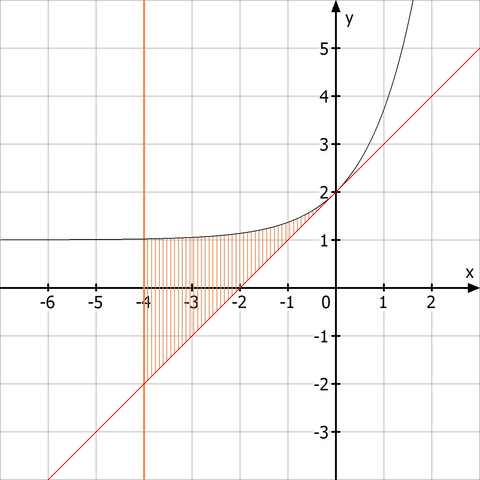
f(x) = e ^ (x) + 1
Der Schnittpunkt mit der y-Achse ist der Punkt (0|2)
Eine Tangente ist eine Gerade, die eine Kurve in einem bestimmten Punkt berührt und dabei die gleiche Steigung wie die Kurve hat.
f´(x) = e ^ x
f´(0) = 1
T(x) = m * x + b
b = T(x) - m * x
m = f´(0) = 1
T(0) = 2
b = 2 - 1 * 0 = 2
T(x) = x + 2
Wir haben außerdem die Gerade x = -4
---------------------------------------------------------------------------------------------------
Die Grenzen verlaufen von -4 bis 0
f(x) liegt betragsmäßig im genannten Intervall über dem Betrag von T(x)
h(x) = f(x) - T(x)
H(x) = ∫ h(x) * dx
h(x) = e ^ (x) + 1 - (x + 2)
h(x) = e ^ (x) - x - 1
H(x) = ∫ h(x) * dx = ∫ (e ^ (x) - x - 1) * dx = e ^ x - (1 / 2) * x ^ 2 - x + C
C = 0
H(x) = e ^ x - (1 / 2) * x ^ 2 - x
A = Flächeninhalt
A = H(0) - H(-4)
H(0) = e ^ 0 - (1 / 2) * 0 ^ 2 - 0 = 1
H(-4) = e ^ (-4) - (1 / 2) * (-4) ^ 2 - (-4) = -3.9816843611112658197
H(0) - H(-4) = 1 - (-3.9816843611112658197) = 4.9816843611112658197
A = 4.9816843611112658197
skizze, tangentengl. im Punkt (0;2) aufstellen; Nullstelle von tangente g berechnen
(-2) dann integrieren von -4 bis 0 mit (f-g)