Wie berechnet man Integral zw. Tangente?
Hallo,
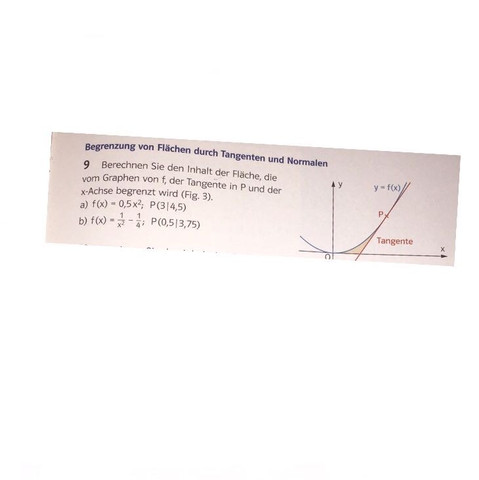
Kann mir jmd. sagen, wie man diese Aufgabe löst? ich habe bald eine Klausur und verstehe nicht, wie man das macht wenn die Fläche so eingegrenzt ist...
2 Antworten
Möchtest du wissen, wie man allgemein ein Integral und eine Tangente berechnen kann oder wie man mit diesen beiden Methoden die Aufgabe löst?
Siehe der Kommentar von Ellejolka (evtl. unter der falsche Antwort gelandet?)
die orange Fläche fängt bei 0 an, da f durch den Ursprung verläuft.
Und x-Wert des Dreiecks ist 3-1,5 = 1,5
Ich habe erstmal die Tangentengleichung dazu ausgerechnet und T(x)=3x-4,5 rausbekommen, jetzt weiß aber nicht, wie mir das weiterhilft.
Ich weiß also nicht wie man das Integral berechnet, dessen Fläche zwischen dem Graph und Tangente eingeschlossen ist
Berechne das Integral von 0 bis 3.
Dann kennst du die gesammte Fläche unter dem Graphen von 0 bis 3.
Bilde nun ein rechtwinkliges Dreieck mit der Tangente, der x-Achse und einer zur x-Achse senkrecht stehenden Geraden durch P.
Der Flächeninhalt dieses Dreiecks lässt sich mit einfacher Geometrie lösen.
Hast du nach diesen beiden Schritten eine Idee was du nun machen musst, um die gefärbte Fläche zu bestimmen?
du integrierst f von 0 bis 3
und ziehst das Dreieck, was die Tg bildet ab; Nullstelle von Tg = 1,5
also 1/2 * (3-1,5) * 4,5
die orange Fläche fängt bei 0 an, da f durch den Ursprung verläuft.
Und x-Wert des Dreiecks ist 3-1,5 = 1,5
Aber warum von 0 bis 3 ? Die orangene fläche fängt doch erst nach 0 an.
Und wenn ich ein dreieck bilde habe ich doch gar keinen x wert davon