Differenzialrechnung - Funktion 4. Grades (Aufgabenstellung)?
Eine ganzrationale Funktion 4. Grades hat bei -1 eine doppelte Nullstelle und bei 2 eine Sattelstelle. Die Tangente im Sattelpunkt hat die Gleichung t(x)= 6,75.
Wie muss man als erstes vorgehen?
ax^4+bx^3+cx^2+dx+e ?
...
(x+1)² = (Doppelte Nullstelle)
(x-2)³ = (Sattelpunkt / Stelle) -> Sattelpunkt heißt man hat nur einen Wert gegeben in diesem Fall x=2 oder?
Ich hoffe Ihr könnt mir dazu weiterhelfen.
3 Antworten
(x-2)³ = (Sattelpunkt / Stelle) -> Sattelpunkt heißt man hat nur einen Wert gegeben in diesem Fall x=2 oder?
Sattelpunkt heißt, die Ableitung ist in dem Punkt 0, aber man hat keine Extremstelle. Also hat die Ableitung keinen Vorzeichenwechsel und somit ist die zweite Ableitung auch 0. Mit der Tangente ist die y-Koordinate des Sattelpunktes angegeben.
Bedingungen:
(1) f(-1) = 0
(2) f'(-1) = 0
(3) f(2) = 6,75
(4) f'(2) = 0
(5) f''(2) = 0
Das führt zu einem LGS, bestehend aus 5 Gleichungen und 5 Unbekannten.
Zum Beispiel so:
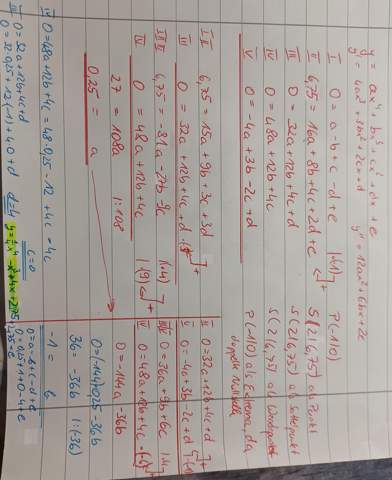
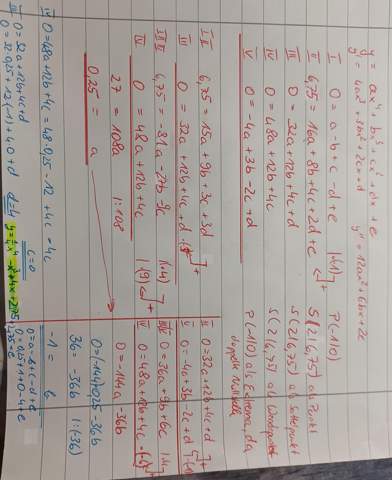
also f´(2)= 0 ?