Die natürliche Exponentialfunktion?
Hallo zusammen
Hier ist die Aufgabe und meine Fragen. Ich bitte Euch die Lösungsansätze klar nachvollziehbar zu erklären, danke.

Und hier ist die Lösung, die ich nicht wirklich verstehe:

Kann mir jemand helfen?
Vielen lieben Dank im voraus.
lg W.
Bitte nicht einfach die Lösung nochmals zitieren. Ich kann ja auch lesen. Mich interessiert, wieso:
- der Differenzialquotient: e^x = e^x sein soll.
- Wieso e^x0 = (e^x0+1/3) sein soll.
- Wieso ist schlussendlich f'(x) = e^2/3?
Bitte - wie gesagt - auf diese Fragen eingehen. Vielen lieben Dank. lg W.
2 Antworten
Zuerst veranschauliche mir die Situation, in dem ich den Graphen zeichne und den Punkt A eintrage. Die Grafik ist sogar schon gegeben. Ich beginne mit der allgemeinen Tangentengleichung t(x) = mx + b
Ich nehme hier eine beliebige Tangente, die durch den Ursprung geht, die hat dann die Form t(x) = mx mit b = 0
(Hier ist m = 1 gewählt, nur für die Grafik, das wird später errechnet)
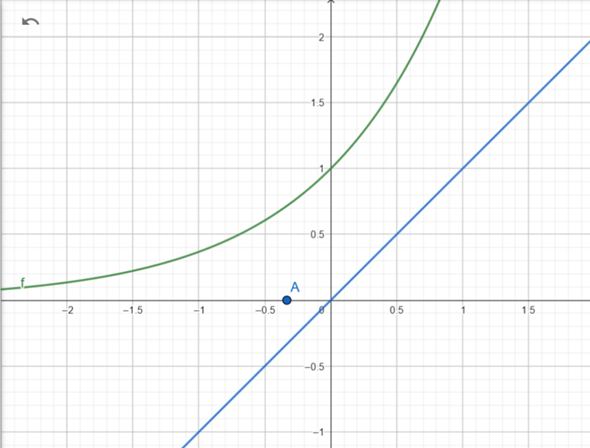
Die Tangente soll durch den Punkt A gehen. Also muss ich die Gerade einmal um -1/3 nach links verschieben. So komme ich auf t(x) = m * ( x + 1/3)
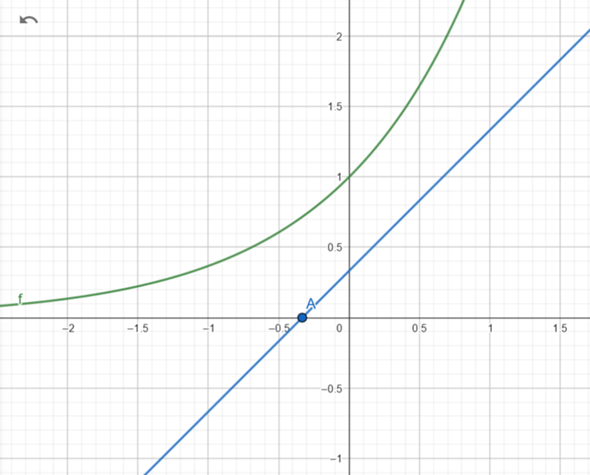
Nun gilt es die Steigung m der Tangente herauszufinden. An der Stelle x0 sollen beide Funktionen die gleiche Steigung haben. Dazu muss ich beide Funktionen einmal ableiten
t(x) = m (x +1/3) = mx + 1/3 * m
t'(x) = m
f(x) = e^x
f'(x) = e^x
An der Stelle x0 sollen beide Funktionen die gleiche Steigung haben. Also gleichsetzen
1) e^x = m
Nicht nur das. Es gibt auch einen gemeinsamen Berührpunkt an dem sich Tangente und Graph treffen. Dessen Stelle errechnet man durch gleichsetzen von f(x) = t(x)
2) e^x = mx + 1/3 * m
Jetzt habe ich zwei Gleichungen für ein Gleichungssystem. Ich wähle zur Lösung das Einsetzungsverfahren. Die erste Gleichung setze ich in die zweite Gleichung ein.
m = mx + 1/3 * m |-m
Jetzt habe ich immer noch 2 Variablen. Hier sieht man schon mal wenn m = 0 ist, habe ich eine Lösung gefunden, da in jedem Term ein m drin vorkommt. Das bestätige ich rechnerisch.
0 = mx + 1/3 * m - m
0 = m ( x + 1/3 - 1) Hieraus folgt m = 0 (das wäre die Lösung im Unendlichen)
Weiter mit der Klammer: x + 1/3 - 1 = 0
x - 2/3 = 0
x = 2/3
An der Stelle x0 = 2/3 gibt es den Berührpunkt. Welche Steigung hat dort f(x) ? Die Steigung am Berührpunkt muss die Steigung der Tangente sein. Tangente und Funktion haben dort die gleiche Steigung. (Eigenschaft einer Tangente)
f'(2/3) = e^(2/3)
Damit ist dort die Steigung m = e^2/3 = 1,9477
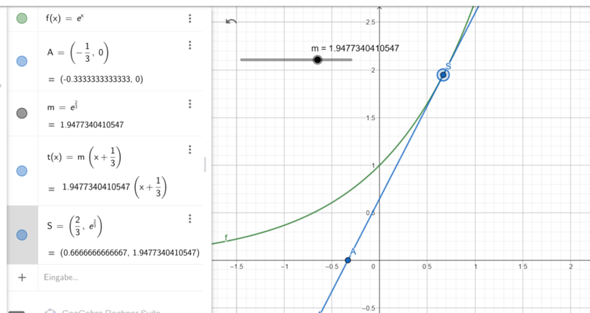
Tangentengleichung:



Dass die Ableitung von e^x = e^x ist, weißt Du bestimmt!
Und wie der Lösungsansatz schon sagt, ist an dem Tangentialpunkt die Ableitung (also e^x) gleich der Steigung des eingezeichneten Dreiecks, also des Differenzenquotienten (y2-y1)/(x2-x1)
y2 ist die Höhe bei B. Die ist e^x
y1 ist die Höhe bei A. Die ist Null
x2 ist die Breite (immer vom Nullpunkt aus gemessen) von B. Die ist x0
x1 ist die Breite von A. Die ist -1/3
Damit ergibt sich die Gleichung die da steht.
sehr gut erklärt