cos(alpha + 90grad) = -sin(alpha)?
Ich verstehe nicht wiso z.B
cos(alpha + 90grad) = -sin(alpha).
Weitere Beispiele :
7 Antworten
Hi Certas,
das wäre der streng trigonometrische Beweis:
cos (α + β) = cos α * cos β - sin α * sin β
da hier β = 90°, haben wir:
cos (α + 90°) = cos α * cos 90° - sin α * sin 90°
da cos 90° = 0 und sin 90° =1, bleibt:
cos (α + 90°) = - sin α
LG,
Heni
Alternativ zum Einheitskreis:
Schau dir die Sinus-und Cosinusfunktion auf einem Graphen aufgezeichnet an, also als "Welle". Dann siehst du, dass der einzige Unterschied ist, dass die cosinusfunktion um pi/2 verschoben ist zur Sinusfunktion. Pi/2 sind 90 Grad (2pi = 360grad ). Dann überprüf deine Gleichungen mal anschaulich und es wird Sinn machen:)
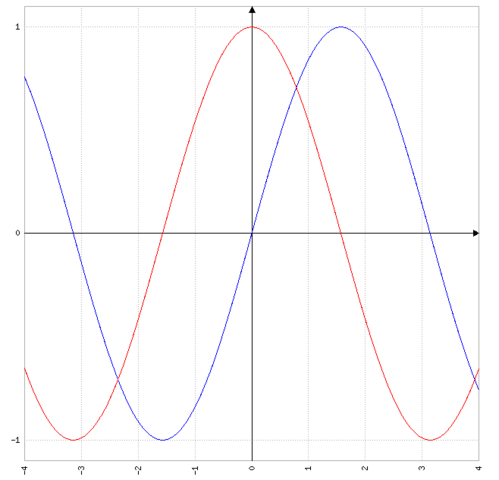
Das Blaue is der Sinus, das Rote der Kosinus.
verschiebst du den Kosinus um 90° nach rechts, hast du den Sinus, verschiebst du ihn um 90° nach links (wie bei dir), dann hast du den - Sinuns
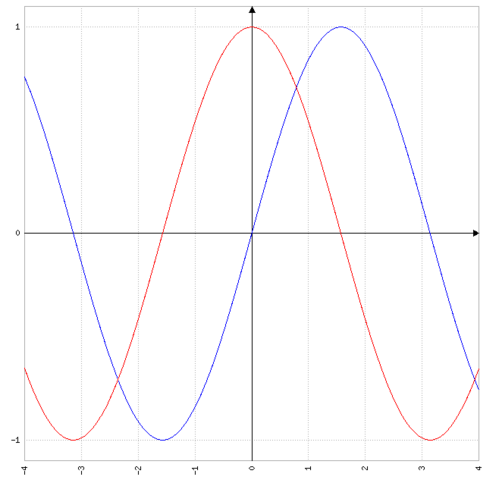
Weil der einzige Unterschied zwischen Sinus und Cosinus nur eine Phasenverschiebung um 90 Grad ist.
Du kannst du Cosinus immer darstellen, als einen Sinus mit 90° Phasenverschiebung.
kann man das logisch schlussfolgern oder muss man dafür die Phasenverschiebung betrachten
Das kann man logisch Schlussfolgern indem man sich die Bildung von Sinus und Cosinus am Einheitskreis ansieht.
Der Cosinus wird zum Sinus sobald man das Koordinatensystem einfach um -90° dreht.
Schau dir die Funktionen mal an,
dann siehst du es schon.
danke ! Mir geht es einfach darum ob man dies irgendwie aus dem kopf kann oder ob man es nachschauen oder berechnen muss