Ähnlichkeitsfaktor bestimmen Hilfe! |Ähnlichkeit von Dreiecken?
Hey :)
ich lerne gerade für Mathe (9. Klasse).
Wir arbeiten momentan das Thema Ähnlichkeiten durch.
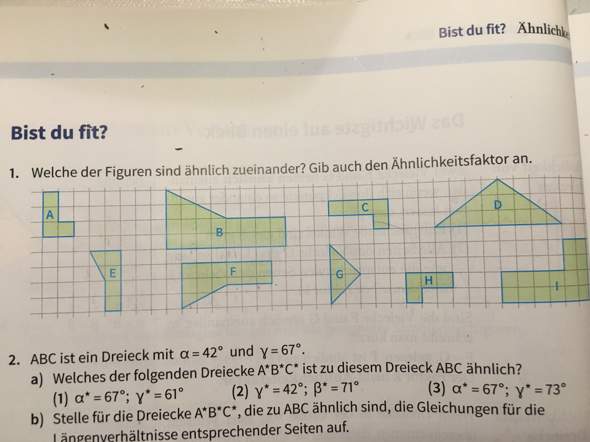
ich habe hier (siehe Bild) die Aufgabe 1)
nun sehe ich, dass Figur E ähnlich zu F ist.
in der Lösung steht
E~F, K= 3/4
F~E,K= 2/3
wie kommt man auf dieses Ergebnis ich verstehe es nicht ganz.
Gibt es eine Rechnung?
Und warum steht es genau in der Reihenfolge ?
Ich freue mich sehr über hilfreiche Antworten:)
3 Antworten
"F~E" heißt : F ist ähnlich zu E. Welche Figur als Original angesehen wird, ist m.E. nicht unbedingt eindeutig.
Hier steht aber "F~E,K= 2/3". Da E kleiner ist als F, müsste F als das Original angesehen werden. Denn k gibt an, mit welchem Faktor ich jede Teilstrecke von F multipliziert werden muss, um auf die Längen der Bildfigur zu kommen. (Dazu misst Du entsprechende Längen aus und bildest dann den Quotienten.)
Umgekehrt dann "E~F, K= 3/4" Hier wird E als Original angesehen. Jedoch muss hier k = 3/2 sein, also genau der Kehrwert des anderen Streckfaktors. Offensichtlich liegt hier ein Tippfehler vor (Deiner oder einer im Buch)
Ist's nun klar?
B und E sind auch ähnlich, und H und I auch.
K ist der gefragte Ähnlichkeitsfaktor und es steht genau in dieser Reihenfolge, weil es im Aufgabentext in dieser Reihenfolge gefragt wurde.
Eine Rechnung gibt es nicht. Den Faktor sieht man doch sofort, wenn man die Kästchen abzählt, die die beiden Figuren begrenzen. Deshalb habe sie es ja auf Karopapier gedruckt. damit die Unfähigen nicht mit dem Lineal nachmessen müssen und dann noch Brüche rechnen müssen.
sorry ... kapiere jetzt erst deine Frage nach der Reihenfolge, Du meintest: warum die Reihenfolge E~F geschrieben wird und nicht F~E, stimmts?
Man kann es so oder so schreiben, aber dann dreht sich natürlich der Faktor rum. "E ist 2/3 so groß wie F" oder auch "F ist 3/2 mal so groß wie E"
übrigens ist da irgendwas falsch, entweder hast Du eine Ähnlichkeit falsch abgeschrieben oder den zugehörenden Faktor