Das wie vielte Glied der Reihe ist das letzte Folgenglied?
Beispiel e)

Bei den vorherigen Beispielen habe ich das letzte Folgenglied immer in das explizite Bildungsgesetz der geometrischen Folge eingesetzt und nach n aufgelöst. Hatte auch funktioniert, aber bei e) und f) klappt’s nicht.
Ich will dadurch auf die Summe der Reihe kommen. Also n in die Summenformel einsetzen.
1/64 = 2 * 0,5^(n-1)
liefert mir aber ein falsches Ergebnis.
Bitte um Hilfe!
2 Antworten
Dein Bildungsgesetz scheint schon falsch zu sein. Ich habe
raus.

Das Vorzeichen vergessen wir mal und rechnen:
Das passt dann auch zur Wertetabelle.
Nachtrag nach Kommentar (leider als Bild, da die Seite die Menge an Formeln nicht akzeptiert)
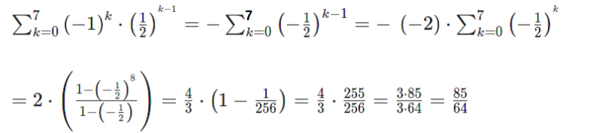

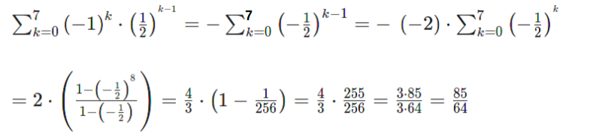
Du hattest gefragt, was das letzte "n" ist und das habe ich beantwortet. Wenn Du die Summe mit der geometrischen Summenformel haben wolltest, dann solltest Du auch das fragen
Ich schreibe dazu einen Nachtrag. Dauert ein wenig.
2 * 0,5^(n-1) . nicht gut . nicht richtig . Hast du ja sicher durch Einsetzprobe schon erkannt
mit n = 0 , 1 , 2
2*0.5^-1 = 2/0.5^1 = 4 !!!
2*0.5^0 = 2
2*0.5^1 = 1
-
Außerdem alternieren die Vorzeichen nicht !
.
Damit das passiert , muss man (-1)^n dabei haben
.
jetzt schaut man , dass man für n = 0 die 2 rauskriegt
.
2*2^n würde das bringen
2*2^1 wäre aber schon der Hinweis auf verkehrt
.
Also mit Basis 1/2 probieren
.
Es steht in der Angabe ich soll mit dem Bildungsgesetz der geometrischen Reihe rechnen.
Die lautet ja an = a1 * q^(n-1)
In die Formel hätte ich eingesetzt und es kommt 4 raus. Und dann soll ich die Summe der Glieder berechnen. Es sollen 85/64 dabei rauskommen.
Aber irgendwie bekomme ich das weder mit n= 4 noch n = 7 :(
Aber danke für deine Hilfe! Ich schätze es sehr!