Wie zeichne ich ein Würfel mit diesen Koordinaten?

Aufgabe a) Ich hab die ersten paar Koordinaten bekommen doch wenn ich G einzeichne macht der Würfel kein Sinn mehr? 😭

Answer 1

[Rammstein53]

@GuteAntwort2021 hat bereits gezeigt, dass die Punkte A,B,G einen Würfel bilden können. Allerdings gebe ich Dir Recht bei der Frage, wie die anderen Punkte eigentlich bestimmt werden können.

Einfach ist das nur dann, wenn man davon ausgeht, dass die Achsen des Würfels parallel zur x-y-z-Achse liegen.

Die Punkte A,B,C,D liegen dann auf der Ebene z = 1, und die Punkte E,F,G,H liegen auf der Ebene z = 5.

Oder die Punkte A,B,E,F liegen auf der Ebene x = 3, und die Punkte D,C,H,G liegen auf der Ebene x = -1

usw.

Darüber sagt die Aufgabe jedoch nichts aus. Streng genommen müsste man erst aufzeigen, dass der Vektor BG einen Winkel von 45° aufweist (was der Fall ist). Nur dann liegen die Punkte A,B,C,D auf der Ebene z = 1. Hätte dieser Vektor einen anderen Winkel, hätte der Würfel eine Rotation erfahren, und die Bestimmung der restlichen Punkte wird sehr umständlich.

Die Aufgabenstellung bewerte ich deshalb mit "ungenügend".

Answer 2

[GuteAntwort2021]

Hallo.

Wieso macht der Würfel dann keinen Sinn mehr?

Sieht doch ziemlich nach einem Würfel aus. 🤷‍♀️

LG

Woher ich das weiß: Studium / Ausbildung – Diplom Wirtschaftsinformatiker

Comments

[Franics617]

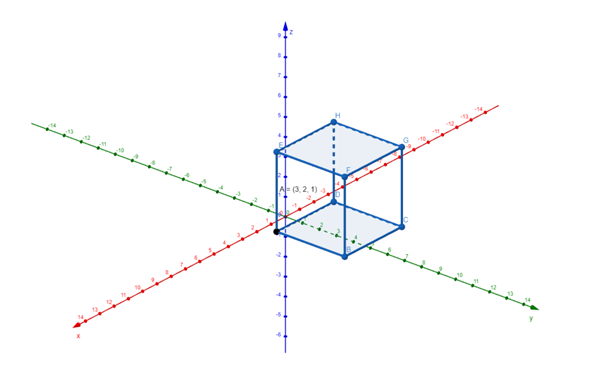
Ich glaube ich hab einfach nicht verstanden wir man die Koordinaten überträgt. 😓 Dankeschön

Answer 3

[xDeniz12]

Der Punkt G passt NICHT zu einem echten Würfel mit AB = 4, weil AG nicht dieselbe Kantenlänge hat. Vermutlich ist G falsch gegeben oder du sollst keinen perfekten Würfel, sondern einen schrägen Quader zeichnen oder die Aufgabe ist absichtlich so gestellt, dass man es bemerkt.

Comments

[GuteAntwort2021]

Der Punkt G passt NICHT zu einem echten Würfel mit AB = 4, weil AG nicht dieselbe Kantenlänge hat.

Natürlich nicht, da es die Hypotenuse von AC und CG ist, wobei AC die Hypotenuse von AB und BC ist. Guck dir die Skizze an. A und B sind die beiden Punkte vorne unten. G hingegen ist hinten oben.

Die Distanz müsste also nach Pythagoras eine Länge von

D = Wurzel(Wurzel(4² + 4²)² + 4²)
D = Wurzel(3*4²)
D = Wurzel(48)

Einheiten zu A haben.

Und wenn wir das überprüfen:

D = Wurzel((3-(-1))² + (2-6)² + (1-5)²)
D = Wurzel(16 + 16 + 16)
D = Wurzel(48)

passt das. G passt also perfekt zum Würfel.

[xDeniz12]

@GuteAntwort2021

Danke für die ausführliche Erklärung! Jetzt verstehe ich auch, warum G trotz des ersten Eindrucks doch passt.

Dass AG nicht dieselbe Länge wie AB hat, hatte mich erst verwirrt, aber du hast recht: G liegt ja nicht direkt entlang einer Kante, sondern bildet mit A und C eine Raumdiagonale. Die Hypotenusen-Argumentation mit AC und CG macht total Sinn, und dass du es mit dem Pythagoras nachgerechnet hast, zeigt es ganz klar:

Die Distanz von A zu G entspricht der Raumdiagonale mit Wurzel(48), und die Rechnung mit den Koordinaten bestätigt das.

Danke nochmal, richtig gut erklärt!