Wie würde man vorgehen um diesen Ausdruck zu integrieren?
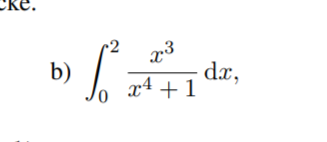
1 Antwort
Integration durch Substitution.
Man setze u := x⁴.
Daraus folgt du/dx = 4x³ bzw. dx = du/(4x³).
Setzen wir das für x⁴ und dx ein, erhalten wir x³/(u+1) du/(4x³).
Du musst also nun 1/(u+1) integrieren, wobei der Faktor 1/4 aus dem Integral gezogen wurde.
Die Lösung ist dann ln(|u+1|)/4+c. Nach den Logarithmusgesetzen kannst du die 1/4 als vierte Wurzel von u+1 in den Logarithmus schreiben - wenn du magst, ich tue es nicht.
Nun müssen wir resubstituieren. Wir erhalten unsere Stammfunktionen ln(x⁴+1)/4+c, wobei der Betrag weggenommen werden kann, da x⁴+1 positiv ist.
Setzt du nun die Grenzen ein und rechnest alles aus, solltest du auf ln(17)/4 kommen.
Müssten die heute nicht Mathe-Hacks heißen ?
Oder auch 5er-Bremse oder DeLigt-Grätsche :-).
Wann trifft eigentlich Bayern auf Werder in der CL?
Da die Funktion bereits "fast" in der Form u'/u vor liegt kann man eine einfachere Regel verwenden, die auch in den meisten Formelsammlungen für Schülerinnen und Schüler vorhanden sein dürfte. Richtig sind deine Ausführungen natürlich trotzdem.