Wie kann man nochmals interpolieren bei 0,1 bar sind es 45,84Grad und bei 0,12 bar sind es 49,45Grad und brauche Temp. bei 0,1141 bar?

Leg eine Gerade durch die beiden Punkte (0.1|45.84) und (0.12|49.45) und setze dann x=0.1141 ein. Es gibt dafür sogar eine fix&fertige Formel. Ich gebe sie Dir in zwei Va­ri­anten: Die erste Variante ist leicht abzuleiten (eine Art finites Differential), die zwei­te ist leichter zu merken, weil sie symmetrisch in den beiden Punkten ist, und sie kann auch ohne viel Mühe auf quadratische oder ku­bi­sche Interpolation verallgemei­nert wer­den („Lagrange-Interpolation“).

Du bekommst y=48.385 °C.

P.S.: Weil ich oben angesprochen habe, daß die Formel auch für höhere Interpola­tions­grade verallgemeinerbar ist, gebe ich der Vollständigkeit halber die Formeln an. Wenn Du drei Punkte hast, dann verwendest Du mit Vorteil die quadratische Interpolation:

und wenn Du Dir das genauer ansiehst, dann erkennst Du, daß die Terme ganz sy­ste­matisch gebaut werden. Im Zähler den i-ten Bruchs stehen die Produkte (xⱼ−x) und im Nenner (xⱼ−xᵢ) für alle j≠i. Die allgemeine Form lautet also

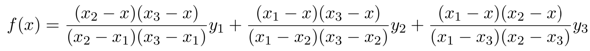
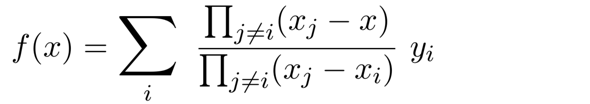
Man kann sich das auch über einen Dreisatz herleiten:

Als Ausgangsbasis nehmen wir p = 0,1 und T = 45,84 °C

Und rechnen da die neue Differenz dazu.

Die bekannte Differenz (= Steigung der Geraden) beträgt für ∆p = 0,02 bar:
49,45 °C - 45,84 °C = 3,61 °C

Dann beträgt die Steigerung für ∆p = 0,0141:
3,61 °C * 0,0141/0,02 = 2,545 °C

Und damit haben wir eine Temperatur von T = 45,84 °C + 2,55 °C = 48,39 °C