Wie kann ich den Rest von 21^30 mod 20 mit einem Taschenrechner ausrechnen?
5 Antworten
Dazu brauchts keinen Taschenrechner. Es gibt da Regeln, wie man das rechnet. Eine davon ist a ≡ b mod m => a^n ≡ b^n mod m. a=21, b=1, n=30 und m=20:
21 ≡ 1 mod 20 (stimmt, also folgt) 21^30 ≡ 1^30 mod 20 und somit (da 1^30=1) 21^30 ≡ 1 mod 20
Versuch´s mal so :
21^30 = ( 20 + 1 )^30Ich hoffe, Du hast schon Ahnung von Binomialkoeffizienten und kannst Dir die Summe zumindest vorstellen:
( 20 + 1 )^30 = 20^30 + a * 20^29 + b * 20^28 + c * 20^27 + .....Alle Potenzen von 20 interessieren ja nicht mod20 , deshalb schaust Du an das Ende der Summe, immer nach Potenzen geordnet:
....... + y * 20^2 + z * 20^1 + 1
Brauchst Du jetzt noch einen Taschenrechner ???
Diese Antwort ist sehr gut, wozu Taschenrechner wenn man Köpfchen gebrauchen kann. Ich wette der Taschenrechner ist "dumm" und wird das Ergebnis garnicht richtig ausrechnen, weil er erst versuchen wird, 21^30 auszurechnen, was viel zu groß ist.
Wenn du die Modulo-Rechengesetze bereits kennst (wenn du also algebraisch bewiesen hast, dass wir hier wirklich einen Ring haben), dann schreibst du einfach:
[21]^30 = [1]^30 = [1^30] = [1], alles mod 20, und bist fertig.
LG
Jeder gute Rechner kennt die PowMod-Funktion, die ohne die ultra extrem großen Zwischenergebnisse auskommt.
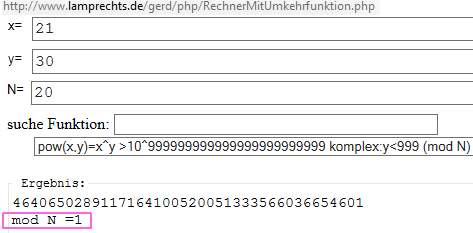
http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php
kann das mit 60 stelligen Zahlen. Diesen Rechner kann man per Handy aufrufen und ist so flexibler als jeder Taschenrechner -> Bild 1
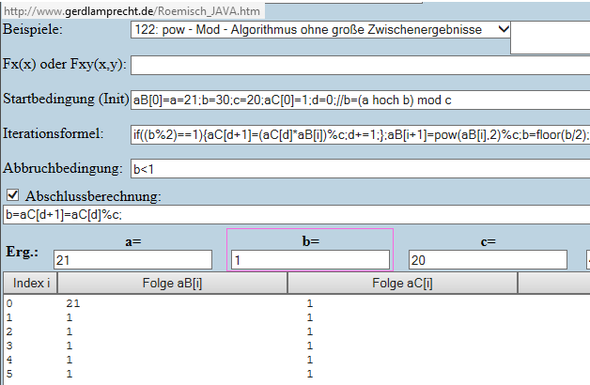
Wie dieser Algorithmus funktioniert zeigt der Iterationsrechner im Beispiel 122:
http://www.gerdlamprecht.de/Roemisch_JAVA.htm
Einfach Variablen a, b und c anpassen -> Bild 2
(mod ist in vielen Sprachen das % Zeichen)
Die 5 Schritte in Deinem Beispiel kann man fast schon im Kopf...
Gar nicht, denn dazu müsste dein Taschenrechner mit 40 signifikanten Zahlenstellen rechnen können um den Modulo zufriedenstellend ausrechnen zu können. Die meisten Taschenrechnergeräte rechnen aber nur mit 10 Zahlenstellen. Wenn es da noch eine andere Möglichkeit gibt, so kenne ich sie nicht.
Indem du einen guten Taschenrechner nimmst. Zum Beispiel diesen hier:
http://www.wolframalpha.com/input/?i=21%C2%B3%E2%81%B0+mod+20
Alternativ schreibst du 21^(30) um zu (21²)^(15) = ((20 + 1)²)^(15) = (20 * 20 + 2 * 20 + 1)^(15) = (22 * 20 +1)^(15).
Hast du jetzt eine eigene Idee, wie man weiter rechnen kann?
Danke, vor guten 20 Jahren wusste ich das bestimmt auch mal. Langsam dämmert es wieder. Könntest du mir noch bitte zur Hilfe einen Lösungsansatz für z.B 2^384 mod 20 geben?